Теорія статистики - Мармоза А. Т. - 11.5. Індексний аналіз

У статистичному аналізі важлива роль належить індексному методу, який дозволяє у відносному та абсолютному виразі оцінити вплив окремих факторів на результативний показник. В основі індексного методу аналізу лежить прийом розкладання індексів змінного складу, які характеризують зміну загального обсягу явища, на індекси постійного (фіксованого) складу, що його складають.

Добуток індексів об'ємного (кількості продукції, площі посіву та ін.) та якісного (ціни, урожайності та ін.) показників дає індекс змінного складу. Зіставляючи між собою індекси змінного і постійного складу, можна визначити вплив структурних зрушень, оцінка впливу яких має велике значення в індексному аналізі складних явищ.

Можливі дві схеми розкладання індексів змінного складу.

І схема.

Спочатку індекс змінного складу розкладається на два індекси постійного складу:

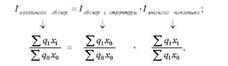
Де Х - якісний показник; д - об'ємний показник.

Потім індекс обсягу і структури розкладають на:

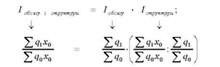
Внаслідок двох етапів розкладання матимемо:

II схема.

Спочатку індекс змінного складу розглядається як добуток індексів обсягу і середнього рівня якісного показника

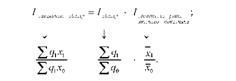
Потім індекс середнього рівня якісного показника знаходять як добуток індексів якісного показника і структури:

Внаслідок двох етапів розкладання матимемо ті самі індекси, що й за І схемою.

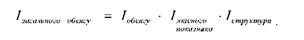
Покажемо практичне застосування зазначених схем аналізу на прикладі індексного методу аналізу валового збору і середньої урожайності зернових культур (табл. 11.8).

За вихідними даними табл. 11.8 потрібно, використовуючи індексний метод аналізу, визначити загальну зміну валового збору зернових культур за два роки і встановити залежність валового збору від розміру і структури посівних площ, середньої урожайності і урожайності окремих культур. Перевірити взаємозв'язок між індексами.

Обчислимо індекс валового збору:

Таблиця 11.8. Площі посіву, урожайність і валовий збір зернових культур в TOB за 2009 - 2010 pp.

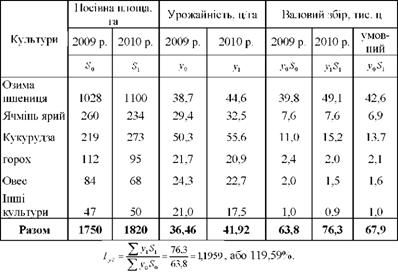
площі посіву, урожайність і валовий збір зернових культур в tob за 2009 - 2010 pp.

Індекс показує, що валовий збір зерна в 2010р. порівняно з 2009р. збільшився на 19,59%.

Для визначення ступеня впливу на валовий збір окремих факторів спочатку розкладемо індекс змінного складу (індекс валового збору) на два індекси постійного складу (урожайності та розміру і структури посівних площ), а потім індекс розміру і структури посівних площ на індекс розміру і індекс структури посівних площ.

Отже, індекс валового збору можна подати як добуток таких трьох індексів:

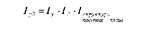
Застосуємо два прийоми розкладу цього індексу.

І прийом аналізу

Подамо індекс валового збору як добуток двох індексів: урожайності окремих культур і розміру і структури посівних площ:

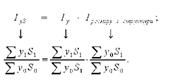
Розкладемо індекс розміру і структури посівних площ на індекс розміру і індекс структури посівних площ:

Визначимо намічені індекси.

Індекс урожайності окремих культур (постійного складу):

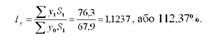
Індекс розміру і структури посівних площ:

Індекс розміру посівних площ:

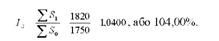
Індекс структури посівних площ:

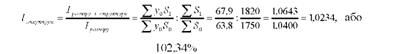
Перевіримо взаємозв'язок індексів і правильність розрахунків:

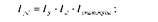
1,1959 = 1,1237-1,0400-1,0234.

Індекси показують, що збільшення валового збору зерна на 19,59% головним чином зумовлено підвищенням урожайності окремих культур на 12,37%, розширенням посівних площ на 4,00% і внаслідок удосконалення структури посівних площ на 2,34%. Удосконалення структури посівних площ означає збільшення в 2010 році порівняно з 2009 р. в загальній посівній площі зернових культур площі культур з вищою урожайністю.

II прийом аналізу

У зв'язку з тим, що посівні площі однорідних культур порівнянні і їх можна підсумовувати, валовий збір зернових культур можна подати як добуток середньої урожайності на посівну площу:

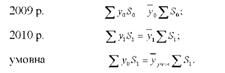
Виходячи з цього, індекс урожайності і індекс структури посівних площ можуть бути розраховані за формулами не агрегатних індексів, а індексів середніх рівнів.

У 5

Поділивши індекс урожайності постійного складу на ~; 1 , отримаємо індекс середніх рівнів урожайності в 2010 р. і умовну

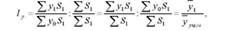
Де У1 і У ,мо, - відповідно середня урожайність в 2010 р. і умовна

Індекс структури посівних площ через середні рівні може бути поданий в такому вигляді:

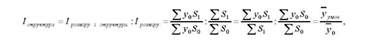
Де у0 середня урожайність в 2009 р.

Відмінність урожайності уума^ і у0 зумовлена тільки структурою посівних площ, оскільки урожайність по окремих культурах є фіксованою (за базисним роком). Тоді індекс валового збору можна розкласти таким чином:

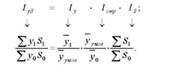
Визначимо середню урожайність за 2009 р., 2010 р. і умовну:

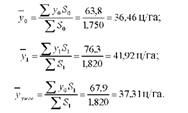
Обчислимо необхідні індекси:

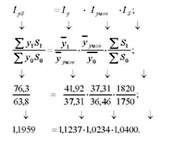
Таким чином, маємо ті самі індекси, що й у першому прийомі аналізу.

Наявність обчислених індексів дає змогу провести аналіз зміни середньої урожайності, яка залежить безпосередньо від двох факторів: урожайності окремих культур і структури посівних площ:

Індекси показують, що середня урожайність в 2010 р. порівняно з 2009 р. підвищилась на 14,98% здебільшого внаслідок зростання урожайності окремих культур на 12,37%, а також внаслідок удосконалення структури посівних площ на 2,34%.

Схожі статті




Теорія статистики - Мармоза А. Т. - 11.5. Індексний аналіз

Предыдущая | Следующая