Теорія статистики - Мармоза А. Т. - 8.2. Дисперсійний аналіз при групуванні даних за однією ознакою
Порядок проведення дисперсійного аналізу при групуванні даних за однією ознакою розглянемо на такому прикладі.
В досліді вивчався вплив нових комбікормів на прирости живої маси бройлерів (табл. 8.1).
Таблиця 8.1. Середньодобові прирости живої маси бройлерів, г
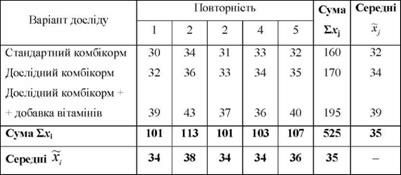
Аналіз даних таблиці показує, що середні прирости живої маси вище по групах бройлерів, що одержували дослідний комбікорм і дослідний комбікорм з добавкою вітамінів. Отже, варіація середніх по варіантах досліду зумовлювалась різним складом раціонів. Але прирости живої маси варіювали і всередині груп, тобто мала місце внутрішньогрупова (залишкова) варіація, викликана рештою неврахованих факторів. Про це свідчать середні прирости живої маси по повторностях: вони коливаються від 34 до 38 г.
На основі вихідних даних методом дисперсійного аналізу перевіримо вірогідність впливу різних за якістю раціонів на прирости живої маси бройлерів. Для цього висунемо і перевіримо статистичну гіпотезу відносно середніх в генеральних сукупностях.
Сформулюємо нульову і альтернативну гіпотези:
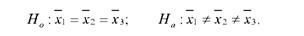
Рівень значущості приймемо рівним а = 0,05. Найпотужнішим критерієм перевірки Но є Б-критерій Фішера. Для перевірки Н0 і формулювання висновків за результатами дисперсійного аналізу необхідно обчислити фактичне значення Б-критерію Фішера і порівняти його з табличним значенням Ба.
Для розрахунку фактичного значення Б-критерію виконаємо всі необхідні операції по його обчисленню відповідно до етапів дисперсійного аналізу.
При групуванні даних за однією ознакою загальний обсяг варіації можна розкласти на варіацію, пов'язану з дією групувальної ознаки (міжгрупову або систематичну), і варіацію внутрішньогрупову (залишкову):
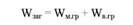
Для визначення сум квадратів відхилень піднесемо до квадрату середньодобові прирости і суми приростів (табл. 8.2).
Позначимо загальне число спостережень N = 15, число варіантів досліду Т = 3, число повторностей П = 5, N = т o п = 3 o 5 = 15.
Таблиця 8.2. Квадрати середньодобових приростів живої маси
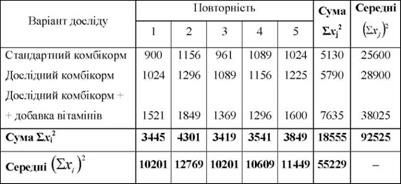
На підставі одержаних в табл. 8.2 даних обчислимо:
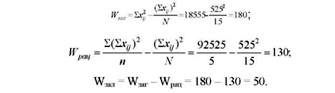
Визначення і розкладання варіації дало такі результати: ™звг = -¥рщ + -¥зал; 180 = 130 + 50 ; 100,0% = 72,2% + 27,8%. Отже, 72,2% загальної варіації середньодобових приростів бройлерів у досліді припадає на варіацію досліджуваного фактора (раціонів), а 27,8% варіації зумовлено неврахованими факторами.
Встановимо число ступенів свободи варіації для кожної суми квадратів відхилень при N = 15, т = 3, п = 5.
Тоді число ступенів свободи варіації для загальної суми квадратів відхилень

Для залишкової визначається за різницею так само, як і залишкова варіація: к2 = к0 - к1 = N - 1) - (т - 1) = 14 - 2 = 12.
Знаючи суми квадратів відхилень і ступені свободи, визначимо дисперсії, як відношення суми квадратів відхилень до відповідного числа ступенів свободи варіації.
Для дисперсійного аналізу викликає інтерес міжгрупова і залишкова дисперсії, а загальна дисперсія в аналізі участі не бере, тому її не обчислюємо:
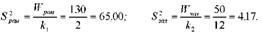
Зіставимо дисперсії, тобто знайдемо фактичне значення Б-критерію Фішера:

Для перевірки нульової гіпотези необхідно визначити табличне значення Б-критерію Фішера (дод. 4) і порівняти його з одержаним фактичним значенням.
V 2
Більшій дисперсії рац відповідає число ступенів свободи варіації КІ =2 (чисельник відношення), меншій дисперсії зал число ступенів свободи варіації к2 = 12 (знаменник відношення). Отже, згідно дод. 4 теоретичне (табличне) значення Б-критерію знаходиться на перетині другого стовпця і дванадцятого рядка: Б005 = 3,88.
Порівняємо фактичне і табличне значення Б-критерію:
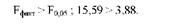
Оскільки Бфакг > Б005, висунута нульова гіпотеза щодо випадкових розбіжностей в групових середніх має бути відхилена і прийнята альтернативна гіпотеза: значення генеральних середніх істотно відрізняються. Іншими словами, фактичні дані не узгоджуються з нульовою гіпотезою. Отже, вплив різних за якістю раціонів на середньодобові прирости живої маси бройлерів вірогідний і істотний.
В дисперсійному аналізі при розкладанні загальної варіації результативної ознаки за компонентами необхідно враховувати порядок формування вибірок: залежні чи незалежні. Якщо в прикладі, що розглядується, вибірки сформовані як незалежні (тобто в кожну групу відібрано по п'ять тварин у випадковому порядку), то загальна сума квадратів відхилень поділяється на два компонента: "¥р! Щ і "¥зал. Однак частіше в дослідах з тваринами формуються групи тварин-аналогів відповідно до числа повторностей по кожному варіанту досліду. Кожен варіант досліду має за повторність - тварину-представника з групи аналогів.
При проведенні експерименту (розглянутий вище приклад) з перевірки впливу різних раціонів на прирости живої маси бройлерів могло бути сформовано п'ять груп тварин-аналогів, оскільки дослід мав проводиться у п'ятикратному повторенні. Групи складалися з трьох голів відповідно варіантам раціону і кожний варіант досліду мав представника з однієї і тієї самої групи тварин-аналогів. Отже, середні по повторностях (по графах табл. 8.1) відбивають тоді відмінності між виділеними групами. Ці відмінності необхідно виключити із загального варіювання приростів, оскільки вони не є випадковими, не пов'язані із зміною раціонів і в певній мірі можуть затушовувати вплив на прирости досліджуваного фактора.
Розкладання загальної варіації результативної ознаки при залежному формуванні вибірок ведеться за схемою:

Тобто на відміну від незалежного формування вибірок включає ще й варіацію повторностей.
За даними табл. 8.2 обчислимо суму квадратів відхилень повторностей:

Цій сумі квадратів відхилень відповідає к"оет = п - 1 = 5 - 1 = 4 тоді дисперсія повторностей становитиме:
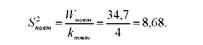
Виключення із загальної суми квадратів відхилень "¥повт призводить і до зміни "¥зал відповідних їй ступенів свободи варіації:
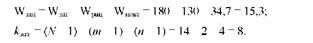
А отже, і залишкової дисперсії
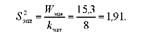
Зіставимо дисперсію раціонів і повторностей із залишковою дисперсією. Результати розрахунків оформимо в табл. 8.3.
Таблиця 8.3. Аналіз дисперсій
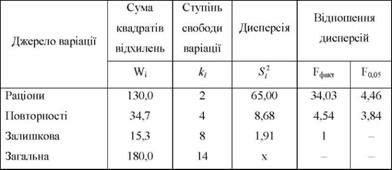
Табличне значення Б-критерію для оцінки відношення дисперсії раціонів до залишкової дисперсії знаходимо на перетині другого стовпця і восьмого рядка - Б005 = 4,46, а для відношення дисперсії повторностей до залишкової - на перетині четвертого стовпця і восьмого рядка - Б005 = 3,84 (дод. 4). Порівняння Рфакг з табличними значеннями призводить до відмови від нульової гіпотези. Отже, відмінності між середніми за раціонами і повторностями не можуть бути віднесені на рахунок випадкового варіювання.
Схожі статті
-
Теорія статистики - Мармоза А. Т. - Розділ 8. Дисперсійний аналіз
8.1. Теоретичні основи і принципова схема дисперсійного аналізу Розглянуті вище прийоми перевірки статистичних гіпотез щодо істотності відмінностей між...
-
Теорія статистики - Мармоза А. Т. - 8.1. Теоретичні основи і принципова схема дисперсійного аналізу
8.1. Теоретичні основи і принципова схема дисперсійного аналізу Розглянуті вище прийоми перевірки статистичних гіпотез щодо істотності відмінностей між...
-
Теорія статистики - Мармоза А. Т. - 7.5. Перевірка статистичних гіпотез щодо розподілів
Поряд з перевіркою статистичних гіпотез щодо середніх інколи потрібно перевірити гіпотези щодо характеру розподілу. Гіпотези про розподіли полягають в...
-
Теорія статистики - Мармоза А. Т. - Розподіл Стьюдента
Теоретичні положення по оцінці вибіркових характеристик на основі малих вибірок (п І - Розподілу Стьюдента. Відхилення вибіркових середніх від...
-
Теорія статистики - Мармоза А. Т. - 5.3. Види дисперсій і правило їх додавання
Дисперсія володіє рядом математичних властивостей, які дають змогу спростити розрахунки. Розглянемо їх. 1. Дисперсія постійної величини дорівнює нулю: Ця...
-
Теорія статистики - Мармоза А. Т. - Розподіл Фішера-Снедекора
Теоретичні положення по оцінці вибіркових характеристик на основі малих вибірок (п І - Розподілу Стьюдента. Відхилення вибіркових середніх від...
-
Теорія статистики - Мармоза А. Т. - Розподіл Пірсона
Теоретичні положення по оцінці вибіркових характеристик на основі малих вибірок (п І - Розподілу Стьюдента. Відхилення вибіркових середніх від...
-
Задача перевірки гіпотези про рівність дисперсій виникає досить часто. Наприклад, при аналізі стабільності виробничого процесу до і після впровадження...
-
Дисперсія володіє рядом математичних властивостей, які дають змогу спростити розрахунки. Розглянемо їх. 1. Дисперсія постійної величини дорівнює нулю: Ця...
-
Теорія статистики - Мармоза А. Т. - 7.4. Перевірка статистичних гіпотез щодо середніх величин
Серед найважливіших узагальнюючих характеристик, відносно яких найчастіше висуваються гіпотези, є середня величина. З метою перевірки гіпотези про...
-
В результаті перевірки статистичної гіпотези, що грунтується на даних вибірки обмеженого обсягу, можна відхилити і прийняти нульову гіпотезу (відповідно...
-
3.1. Поняття про статистичне зведення У результаті першої стадії статистичного дослідження - статистичного спостереження - отримують статистичну...
-
Теорія статистики - Мармоза А. Т. - Середня арифметична
Залежно від характеру усереднюваної ознаки і наявної вихідної інформації в статистиці застосовуються різні види середніх величин, серед яких найбільше...
-
Теорія статистики - Мармоза А. Т. - 4.2. Види середніх величин і способи їх обчислення
Залежно від характеру усереднюваної ознаки і наявної вихідної інформації в статистиці застосовуються різні види середніх величин, серед яких найбільше...
-
Оскільки всі елементи генеральної сукупності для обчислення шуканого параметра, як правило, використати неможливо, то про цей параметр намагаються судити...
-
Теорія статистики - Мармоза А. Т. - 6.4. Визначення необхідної чисельності вибірки
При організації вибіркового спостереження виникає питання про те, якою повинна бути чисельність вибіркової сукупності, при якій межі можливої помилки не...
-
Теорія статистики - Мармоза А. Т. - 7.3. Загальна схема перевірки статистичної гіпотези
Підсумовуючи, можна навести загальну схему (алгоритм) перевірки статистичної гіпотези. Ця перевірка, як зазначалося вище, може бути проведена з...
-
Теорія статистики - Мармоза А. Т. - 3.3. Методологія статистичних групувань
Статистичні групування здійснюють у кілька послідовних етапів: 1) теоретичний аналіз досліджуваного явища або процесу; 2) вибір групувальної ознаки...
-
У процесі збирання статистичних даних можуть виникнути похибки і неточності, які називають Помилками спостереження. Кількісно вони визначаються різницею...
-
Теорія статистики - Мармоза А. Т. - 3.6. Статистичні таблиці
Результати статистичного зведення і групування, як правило, оформляються у вигляді статистичних таблиць. Статистичні таблиці - це форма...
-
Теорія статистики - Мармоза А. Т. - 4.1. Поняття про середні величини
4.1. Поняття про середні величини Статистична сукупність складається з множини одиниць, об'єктів або явищ однорідних в деякому відношенні і одночасно...
-
Теорія статистики - Мармоза А. Т. - Інші види середніх величин
Крім розглянутих вище видів середніх величин, статистикою розроблено і інші види. Середня хронологічна Являє собою середню величину з показників, що...
-
Теорія статистики - Мармоза А. Т. - Розділ 4. Середні величини
4.1. Поняття про середні величини Статистична сукупність складається з множини одиниць, об'єктів або явищ однорідних в деякому відношенні і одночасно...
-
Теорія статистики - Мармоза А. Т. - 6.2. Помилки вибірки
Між показниками вибіркової сукупності і шуканими показниками (параметрами) генеральної сукупності, як правило, існують деякі розбіжності, які називають...
-
Теорія статистики - Мармоза А. Т. - 5.4. Моменти статистичних розподілів
Розглянуті вище середні величини і показники варіації є частковими випадками єдиної системи узагальнюючих статистичних характеристик розподілу, що...
-
Теорія статистики - Мармоза А. Т. - 3.9. Показники диференціації ознак у сукупності
Для вивчення ступеня нерівномірності розподілу певного показника між одиницями окремих груп варіаційного ряду розподілу в статистиці можуть бути...
-
Теорія статистики - Мармоза А. Т. - Абсолютні показники варіації
Найпростішим показником варіації є розмах варіації, який представляє собою різницю між максимальним і мінімальним значеннями ознаки. В інтервальних рядах...
-
Теорія статистики - Мармоза А. Т. - Відносні показники варіації
Найпростішим показником варіації є розмах варіації, який представляє собою різницю між максимальним і мінімальним значеннями ознаки. В інтервальних рядах...
-
Теорія статистики - Мармоза А. Т. - Розмах варіації
Найпростішим показником варіації є розмах варіації, який представляє собою різницю між максимальним і мінімальним значеннями ознаки. В інтервальних рядах...
-
Теорія статистики - Мармоза А. Т. - 5.1. Поняття варіації ознак. Показники варіації
5.1. Поняття варіації ознак. Показники варіації При вивчені масових соціально-економічних явищ і процесів статистика зустрічається з різноманітною...
Теорія статистики - Мармоза А. Т. - 8.2. Дисперсійний аналіз при групуванні даних за однією ознакою