Теорія статистики - Мармоза А. Т. - 4.3. Властивості середньої арифметичної. Розрахунок середньої арифметичної способом моментів

Середня арифметична має ряд математичних властивостей, які можна використати, щоб спростити її розрахунки. Основні властивості середньої арифметичної такі.

1. Середня арифметична постійної величини дорівнює цій постійній:

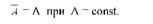
2. Сума квадратів відхилень від середньої арифметичної завжди менша, ніж сума квадратів відхилень від будь-якої іншої величини:

X (Х- X)2 / < (х-А)2 /.

3. Величина середньої не зміниться, якщо частоти ряду розподілу замінити частостями.

4. Сума відхилень окремих значень ознаки від середньої, перемножених на ваги (частоти), дорівнює нулю:

£ (х - х) = Х - пх = 0 - для простої середньої;

£ (х - х)/ = £ х/ - х£ / = 0 - для зваженої середньої.

5. Якщо усі значення ознак збільшити або зменшити у ту саму кількість разів (к), то середня (х) збільшиться або зменшиться у стільки ж разів:

І/ Й У_/ Ь-

Тобто середня зменшилася в (к) разів.

6. Якщо з усіх значень варіант (х) відняти або додати до них ту саму постійну величину (х0), то середня (х) зменшиться або збільшиться на таку саму величину (хо):

У,(Х-хо)/ = 2Х У,Хо/ = -_ ХоУ,/ = -_ І/ І/ І/ Х І/ Х х°"

Тобто середня зменшилася на постійне число х0.

7. Якщо частоти (ваги) поділити або помножити на будь-яке постійне число (к ), то середня не зміниться:

- УХк/ КУХ/ Ух/ -2Ж / £ /

Тобто значення середньої не змінилося.

8. Добуток середньої на суму частот дорівнює сумі добутків варіант на частоти:

XI / = £X/.

Ця рівність випливає з визначальної властивості середньої арифметичної, згідно з якою, зрівнюючи варіанти, надаючи їм однакові значення шляхом заміни їх середнім значенням, незмінним залишається загальний обсяг ознаки.

9. Загальна середня дорівнює середній із часткових середніх, зважених за чисельністю відповідних частин (груп) сукупності:

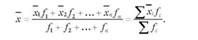
Викладені вище властивості середньої арифметичної дають змогу спростити її розрахунки: можна з усіх значень ознаки відняти довільну постійну величину, одержану різницю поділити на величину інтервалу, а потім обчислену середню помножити на величину інтервалу і додати довільну постійну величину, що прийнята за початок відліку.

Формула обчислення середньої арифметичної спрощеним способом має такий вигляд:

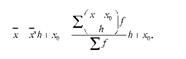
Де Х = --зменшена середня арифметична;

Ф

Х= х к° - відхилення в інтервалах; х0 - початок відліку;

К - величина інтервалу.

Середня Х Із значення - називається моментом першого порядку, а к спосіб обчислення середньої - способом моментів або Способом відліку від умовного початку.

За умовний початок відліку (х0) звичайно приймають одне із значень варіючої ознаки, яке, як правило, знаходиться в центрі ряду розподілу або таке, що має найбільшу частоту.

Розглянемо приклад визначення середньої арифметичної в інтервальному ряду розподілу способом моментів, використовуючи дані про розподіл 100 господарств за надоєм молока на корову (табл. 4.7).

За умовний початок відліку (х0) візьмемо одне із значень інтервалу, розташованого в центрі ряду розподілу і яке має найбільшу частоту. В нашій задачі таким значенням буде х0 = 33 ц. Величина інтервалу К = 2 ц.

За даними таблиці визначимо умовну (зменшену) середню арифметичну:

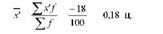
Таблиця 4.7. Дані для розрахунку середньої арифметичної в інтервальному ряду розподілу способом моментів

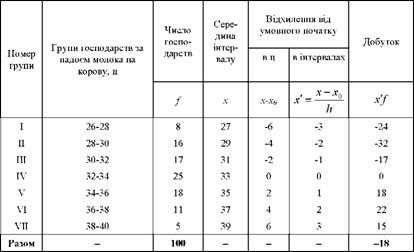
дані для розрахунку середньої арифметичної в інтервальному ряду розподілу способом моментів

Щоб одержати дійсну середню продуктивність корів, необхідно внести відповідні поправки:

Таким чином одержано такий самий результат як і за даними табл. 4.2. Результати розрахунків середньої арифметичної двома способами повністю співпали.

Схожі статті




Теорія статистики - Мармоза А. Т. - 4.3. Властивості середньої арифметичної. Розрахунок середньої арифметичної способом моментів

Предыдущая | Следующая