Теорія статистики - Мармоза А. Т. - 11.3. Найважливіші економічні індекси і їх взаємозв'язок

Крім індексів цін, вартісного і фізичного обсягу продукції в статистиці широке застосування знаходять індекси продуктивності праці, собівартості продукції, урожайності, продуктивності тварин та ін.

Для характеристики зміни продуктивності праці використовуються два індекси продуктивності праці (трудовий і вартісний).

Якщо продуктивність праці виражається показником затрат робочого часу на одиницю продукції, то індивідуальний індекс продуктивності праці будують так:

Де г0 і і1 - затрати робочого часу на одиницю продукції відповідно в базисному і звітному періодах; Т0 = д0і0 і Т1 = д1і1 - затрати робочого часу на всю продукцію відповідно в базисному і звітному періодах; д0 і Ц1 - Кількість виробленої продукції в базисному і звітному періодах.

Агрегатний індекс продуктивності праці (трудовий) виражається формулою:

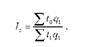
Де £ га ц1 - умовні затрати робочого часу на всю продукцію звітного періоду;

£ ^ - фактичні затрати робочого часу на всю продукцію звітного періоду.

На відміну від наведених вище формул інших агрегатних індексів в цьому індексі базисна величина індексованого показника (га) знаходиться в чисельнику, а звітна величина (г1) - в знаменнику. Це зумовлено тим, що, затрати праці на одиницю продукції і продуктивність праці пов'язані оберненою залежністю.

Тому індивідуальний і агрегатний індекс затрат робочого часу (трудомісткості) мають відповідно вигляд:

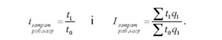
Чим менше затрати робочого часу на виробництво одиниці продукції, тим вищою при інших рівних умовах є продуктивність праці.

Перетворивши агрегатну формулу індексу продуктивності праці заміною Г0 = , Дістанемо середній арифметичний індекс продуктивності праці:

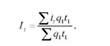
Якщо затрати робочого часу на всю продукцію звітного періоду (Г1ц1 ) позначити через Т1, то наведена вище формула середнього арифметичного індексу продуктивності праці буде мати вигляд:

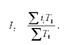
Трудовий індекс продуктивності праці є індексом постійного складу. Він характеризує зміну продуктивності праці за рахунок одного фактора - зміни затрат робочого часу. Якщо індекс продуктивності праці більше одиниці, то різниця між чисельником і знаменником характеризує економію затрат робочого часу за рахунок підвищення продуктивності праці.

Вартісний індекс продуктивності праці Обчислюється за формулою

Де д0 і д1 - кількість продукції звітного і базисного періодів;

£Т =2]І ^Т0 Г Д0 - затрати робочого часу на всю продукцію у

Звітному і базисному періодах;

Р0 - порівнянна (незмінна) ціна за одиницю продукції;

В цьому індексі порівнюються середній виробіток (в гривнях) за одиницю робочого часу за звітний і базисний періоди. Вартістний індекс продуктивності праці є індексом змінного складу. Він характеризує зміну продуктивності праці внаслідок зміни двох факторів - затрат робочого часу на виробництво окремих видів продукції і структури (асортименту) продукції.

Вартісний індекс продуктивності праці можна подати як індекс, що характеризує зміну фізичного обсягу продукції, та індекс затрат робочого часу:

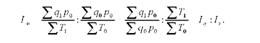
Розрахунок і аналіз індексів продуктивності праці розглянемо на такому прикладі (табл. 11.5).

Співставляючи умовні і фактичні затрати праці на всю продукцію звітного періоду, розрахуємо трудовий індекс продуктивності праці:

Отже, продуктивність праці у звітному періоді порівняно з базисним у середньому підвищилася на 5.28%.

Різниця між чисельником та знаменником індексу £ Г0 ц1 t1ql = 602,5 - 572,3 = 30,2 тис. людино-годин показує економію робочого часу, отриману в результаті зростання продуктивності праці.

Трудовий індекс продуктивності праці може бути розрахований і за формулою середнього арифметичного індексу:

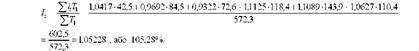
Таким чином, одержано такий самий результат, що й при визначенні агрегатного індексу продуктивності праці.

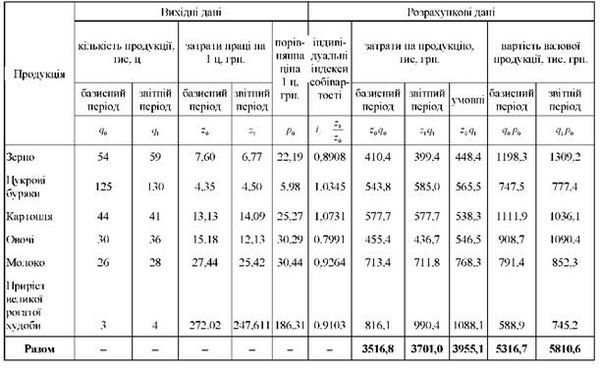
Таблиця 11.5. Дані для розрахунку індексів продуктивності праці

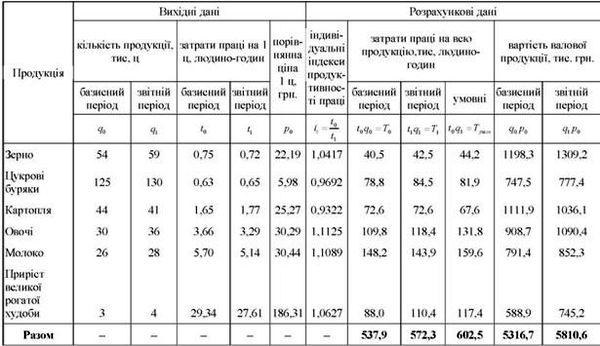
дані для розрахунку індексів продуктивності праці

Співставляючи між собою середні рівні продуктивності праці (виробництво валової продукції у порівнянних цінах на одну людино-годину) за два періоди І ша ), розрахуємо вартісний індекс продуктивності праці:

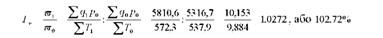
Отже, продуктивність праці у звітному періоді порівняно з базисним підвищилася на 0,269 грн. (10,153 - 9,884), або на 2,72%.

Перетворивши формулу вартісного індексу продуктивності праці, його можна подати як відношення індексів фізичного обсягу продукції і загальних затрат праці:

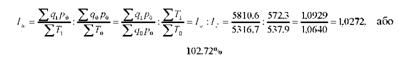
Отже, збільшення фізичного обсягу продукції на 9,29% було забезпечено приростом загальних затрат праці на 6,40%.

Зміна собівартості виробництва окремого виду продукції за два окремих періоди може бути визначена за допомогою індивідуального індексу:

Де и0 і и1 - собівартість одиниці продукції у базисному і звітному періодах, грн.

Для характеристики зміни середньої собівартості у динаміці будують індекс собівартості змінного складу:

Де иі і и0 - середня собівартість одиниці продукції в базисному і звітному періодах; И0 І и1 - собівартість одиниці продукції в базисному і звітному періодах; q0 і q1 - кількість продукції в базисному і звітному періодах.

Цей індекс показує зміну собівартості виробництва продукції внаслідок впливу двох факторів (зміни собівартості і структури продукції) і є індексом змінного складу.

Щоб усунути вплив зміни структури продукції на динаміку середньої собівартості, необхідно розрахувати для двох періодів середню собівартість при тій самій структурі продукції. Для собівартості це фіксування тієї самої структури дістає відображення в такій формулі:

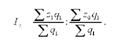
Після скорочення на £ Ц1 цей індекс набуває вигляду формули агрегатного Індексу собівартості постійного складу:

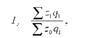
Де 2 Ч ч ~ фактичні витрати на виробництво всієї продукції у звітному періоді; £ И0 Д1 - умовні витрати на виробництво всієї продукції у звітному періоді.

Різниця між чисельником і знаменником індексу показує суму економії від зниження собівартості (якщо різниця матиме знак мінус) або суму перевитрат витрат (якщо різниця матиме знак плюс ).

Індекс собівартості постійного складу характеризує середню зміну собівартості за рахунок одного фактора - зміни самих витрат на виробництво одиниці продукції і не відображує її зміни внаслідок зміни структури продукції.

Для встановлення ступеня впливу структурних зрушень на зміну середньої собівартості обчислюють Індекс структурних зрушень - Відношення індексу змінного складу до індексу постійного складу:

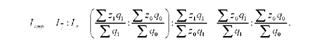
Після перетворення дістанемо:

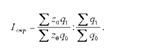
З цієї формули видно, що при випуску однорідної продукції індекс структурних зрушень можна обчислити як відношення індексу фізичного обсягу продукції, сумірною за базисною собівартістю, до індексу фізичного обсягу тієї самої продукції в натуральних одиницях вимірювання.

Між індексами загальних витрат, собівартості та фізичного обсягу продукції існує такий взаємозв'язок, який випливає з такого положення: взаємозв'язки індексів конкретних економічних явищ зумовлені взаємозв'язками відтворюваних ними явищ. Так, загальні витрати на виробництво продукції( Zq ) є добутком собівартості (И ) на обсяг виробленої продукції (Q ). Звідси,

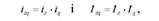
Що підтверджується такою рівністю:

Звідси, індекс фізичного обсягу продукції можна дістати як частку від ділення індексу загальних витрат на індекс собівартості виробництва продукції.

Для характеристики ефективності або окупності витрат використовується Індекс середніх витрат на одну гривню Або тисячу гривень продукції:

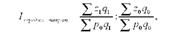
Де р0 - порівнянна (незмінна) ціна одиниці продукції.

Індекс середніх витрат є індексом змінного складу. Він характеризує зміну середніх витрат за рахунок двох факторів: зміни собівартості і структурних зрушень (асортименту продукції).

Індекс середніх витрат можна розкласти на два взаємопов'язаних індекси: індекс загальних витрат і індекс фізичного обсягу і подати так:

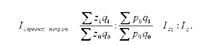
Якщо необхідно визначити ступінь виконання плану по собівартості продукції, розраховують індекс виконання плану по собівартості:

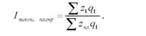
На величину цього індексу впливає не тільки виконання плану собівартості по кожному виду продукції, але й зсув фактичного асортименту продукції (д1) порівняно із запланованим, так як план по зниженню собівартості, звичайно, складено за плановим асортиментом:

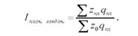
Щоб зсув у асортименті продукції не впливав на показник виконання плану по собівартості, індекс виконання плану слід було б обчислювати з плановими вагами:

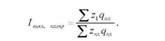
Слід зазначити, що величини індексів продуктивності праці вартісного і середніх витрат залежать не тільки від зміни рівня собівартості і затрат праці на одиницю продукції, але й від зміни складу продукції, тобто співвідношення продуктів з різними витратами на одну гривню продукції або різним її виходом на одиницю часу. Тому індекс середніх витрат на одну гривню і індекс продуктивності праці вартісний слід застосовувати при відсутності істотних відмінностей в складі продукції за два періоди.

Порядок розрахунку індексів собівартості і середніх витрат на одну гривню продукції розглянемо на такому прикладі (табл. 11.6).

Співставляючи фактичні і умовні витрати на виробництво всієї продукції, визначимо агрегатний індекс собівартості:

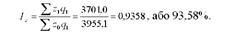
Отже, собівартість виробництва продукції у звітному періоді порівняно з базисним в середньому знизилася на 6,42% (93,58 - 100).

Таблиця 11. 6. Дані для розрахунку індексів собівартості і середніх витрат на одну гривню продукції

дані для розрахунку індексів собівартості і середніх витрат на одну гривню продукції

Різниця між чисельником і знаменником індексу £ и0 q1 =

3701,0 - 3955,1 = - 254,1 тис. грн. показує економію у витратах за рахунок зниження собівартості продукції.

Знаючи індивідуальні індекси собівартості і фактичні витрати на всю продукцію звітного періоду, загальний індекс собівартості продукції можна розрахувати за формулою середнього гармонічного індексу:

Отже, отримано такий самий результат, що й при розрахунку агрегатного індексу собівартості.

Співставляючи між собою середні рівні витрат на одну гривню продукції у звітному і базисному періодах, розрахуємо індекс середніх витрат на одну гривню сукупної продукції:

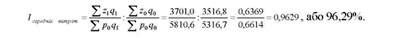
Отже, середні витрати на одну гривню продукції у звітному періоді порівняно з базисним знизилися на 0,0245 грн.(0,6369 - 0,6614), або на 3,71%.

Індекс середніх витрат на одну гривню продукції можна подати як відношення індексів загальних витрат і фізичного обсягу продукції:

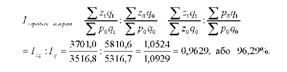
Знайдений індекс показує що загальні витрати на всю продукцію звітного періоду підвищилися на 5,24% при зростанні фізичного обсягу продукції на 9,29%. Більш високі темпи зростання фізичного обсягу продукції (9,29%) порівняно із зростанням витрат на її виробництво (5,24%) призвели до зниження витрат на одну гривню на 3,71%.

За наявними даними можна також обчислити і перевірити взаємозв'язок між індексами загальних витрат, собівартості і фізичного обсягу продукції за собівартістю:

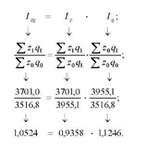
Отже, загальні витрати на виробництво продукції у звітному періоді порівняно з базисним зросли в середньому на 5,24%. Це зростання відбулося внаслідок зростання фізичного обсягу продукції на 12,46 % при зниженні собівартості продукції на 6,42%.

Аналогічно побудові індексів собівартості будують індекси урожайності і продуктивності тварин. Смисл і зміст індексів урожайності розглядується в параграфі 11.5 даного розділу.

Схожі статті




Теорія статистики - Мармоза А. Т. - 11.3. Найважливіші економічні індекси і їх взаємозв'язок

Предыдущая | Следующая