Теорія статистики - Мармоза А. Т. - 8.4. Дисперсійний аналіз при групуванні даних за двома ознаками

В статистичній практиці частіше мають справу з багатофакторними дослідами, в яких вивчають вплив на результативну ознаку двох і більше факторів одночасно.

За аналогією з комбінаційними групуваннями багатофакторні моделі дисперсійного аналізу мають незаперечну перевагу порівняно з однофакторними моделями: вони дають змогу виявити ступінь впливу не тільки кожного фактора окремо, а й їхню взаємодію. Наприклад, ефективність добрив підвищується при покращенні догляду за рослинами, переваги високоврожайних сортів повністю проявляються при високій агротехніці їх вирощування. Ці завдання розв'язуються за допомогою побудови комбінаційних групувань і таблиць. Методи ж розкладання варіації дають числові характеристики взаємодії факторів, а використання імовірнісних оцінок дає змогу зробити висновок про її вірогідність.

Дисперсійний аналіз при групуванні даних за двома факторами ведеться за тією самою принциповою схемою, що й при групуванні даних за одним фактором. При цьому також необхідно враховувати порядок формування груп: випадкове чи невипадкове (незалежні чи залежні вибірки). При залежному формуванні вибірок схема розкладання суми квадратів відхилень ускладнюється в зв'язку з виділенням суми квадратів відхилень повторень.

Відмінність багатофакторного аналізу від однофакторного полягає в тому, що загальний обсяг варіації розкладається на більше число компонентів. В міру розкладання сукупності на групи і підгрупи ускладнюються розрахунки з розкладання загального обсягу варіації на складові частини, а також аналіз дисперсій.

Розглянемо схему розкладання загальної варіації на складові частини для випадку з двома факторами (А і В). Джерелами варіації при групуванні даних за двома факторами будуть: перший фактор - А, другий фактор - В, їх взаємодія - АВ, залишкове варіювання.

Тоді загальну суму квадратів відхилень можна подати в такому вигляді: "¥заг = "¥А + "¥в + "¥АВ + "¥зал.

Розкладання загальної варіації доцільно здійснити в два етапи. Для цього потрібно побудувати дві таблиці. На першому етапі із загального варіювання слід виділити варіацію, пов'язану з двома факторами і залишкову варіацію:

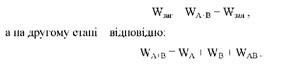
Такий порядок розкладання загальної варіації справедливий для незалежних вибірок. Якщо ж вибірки залежні (наприклад, рендомізовані блоки, латинський квадрат тощо), то з'являється новий компонент варіації, пов'язаний з повторностями

Тоді схема розкладання загальної варіації набуває такого вигляду:

I етап "¥заг = "¥А+В + "¥повт + "¥зал ;

II етап "¥А+В = "¥А + "¥в + "¥АВ ;

І в цілому Шзяг = "¥А + "¥в + "¥АВ + "¥повт + "¥зал.

Для випадку з трьома факторами і залежними вибірками схема розкладення загальної варіації ускладнюється:

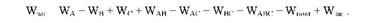
Факторні моделі з великою кількістю факторів (трьома і більше) доцільно досліджувати кореляційним методом з використанням ЕОМ.

Використання дисперсійного аналізу при групуванні даних за двома факторами розглянемо на такому прикладі. В польовому досліді вивчався вплив різних доз добрив на урожайність озимої пшениці, висіяної на ділянках з різними попередниками (табл. 8.5).

Таблиця 8.5. Урожайність озимої пшениці, ц/га

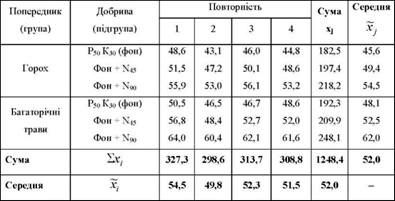
урожайність озимої пшениці, ц/га

Схема побудови досліду така: ділянку, на якій проводився дослід, було розбито на чотири блоки, що відрізняються між собою рельєфом і механічним складом грунтів. Кожен з варіантів досліду у випадковому порядку було розподілено в усіх чотирьох блоках, чим зумовлювалося значне вирівнювання умов в усіх перевірюваних варіантах досліду. Отже, дослід проведено в чотирьохкратній повторності і побудовано за методом рендомізованих блоків (залежні вибірки).

Потрібно методом дисперсійного аналізу перевірити статистичну гіпотезу відносно середніх у генеральних сукупностях.

Порівнюючи середню урожайність по групах (попередниках) і підгрупах (добривах), можна помітити, що урожайність озимої пшениці закономірно зростає по мірі зміни попередника і збільшення доз добрив. Разом з тим висунемо нульові гіпотези про випадковість відмінностей середньої урожайності за варіантами досліду, тобто про те, що фактори не впливають на рівень урожайності озимої пшениці:

В) Н0: ефективність взаємодії факторів у генеральних сукупностях однакова;

На: ефективність взаємодії факторів у генеральних сукупностях неоднакова;

Тут хі - середні по групах; Х] - середні по підгрупах.

Рівень значущості візьмемо таким, що дорівнює а = 0,05. Для перевірки Но використаємо критерій Б.

Схема побудови досліду показує, що загальну варіацію урожайності озимої пшениці можна розкласти на 5 компонентів:

Де "¥заг - варіація урожайності за рахунок впливу: попередників ¥п, добрив ¥д, взаємодії факторів (попередників і добрив) "¥вз, повторностей "¥повт; "¥зал - залишкова варіація.

Розкладання загальної варіації проведемо в два етапи. На першому етапі виділимо із загальної варіації

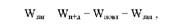
Тобто варіацію, що створюється спільним впливом попередників і добрив, варіацію по блоках (повторностях) і залишкову (відхилення індивідуальних спостережень від середніх по кожному фактору окремо).

На другому етапі виділимо варіацію (суму квадратів відхилень), пов'язану з дією факторів (кожного окремо і їхню спільну взаємодію):

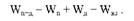
Позначимо число спостережень в досліді N = 24, кількість груп за попередниками Т = 2, кількість підгруп за добривами І = 3 і за блоками п = 4 N = тІп = 2 o 3 o 4 = 24).

Для спрощення обчислень сум квадратів відхилень зменшимо всі вихідні дані на постійну величину, близьку до середньої величини (а = 50) і виразимо дані досліду у відхиленнях від постійної величини.

Результати обчислень запишемо в табл. 8.6.

Таблиця 8.6. Відхилення від умовного початку (у = Х - а; а = 50)

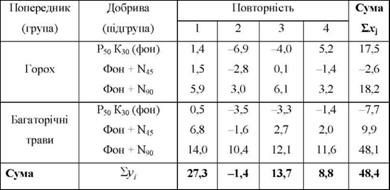
відхилення від умовного початку

Перевіримо правильність розрахунків: загальна сума урожайності (іх,7 = 1248,4) має дорівнювати сумі відхилень від умовного початку = 48,4), плюс добуток умовного початку на кількість спостережень (атУ):

Для визначення сум квадратів відхилень "¥заг; "¥п+д; "¥повт і Wзaл піднесемо до квадрата всі індивідуальні відхилення, їх суми по графі і рядку і

Загальний підсумок (табл. 8.7).

Таблиця 8.7. Квадрати відхилень

квадрати відхилень

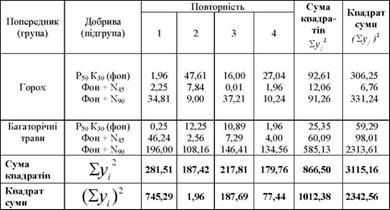
В результаті піднесення до квадрата відхилень отримаємо всі потрібні дані для визначення сум квадратів відхилень на першому етапі:

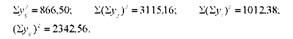
Користуючись одержаними сумами, визначимо необхідні суми квадратів відхилень:

Для кожної суми квадратів відхилень визначимо число ступенів свободи варіації:

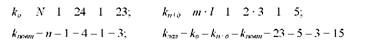
На другому етапі проведемо розкладання варіації, пов'язаної з дією факторів (за рахунок кожного фактора та їх взаємодії):

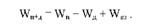
Для розрахунку необхідних сум квадратів відхилень на підставі даних останнього стовпця табл. 8.6 складемо нову таблицю відхилень (табл. 8.8), в якій назви рядків містять градації за попередниками, а стовпців - за дозами добрив. Позначимо суми відхилень за попередниками - А, а за дозами добрив - В і піднесемо до квадрата відхилення (табл. 8.9).

Таблиця 8.8. Відхилення по варіантах досліду

відхилення по варіантах досліду

Таблиця 8.9. Квадрати відхилень по варіантах досліду

квадрати відхилень по варіантах досліду

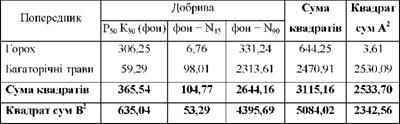
Сума квадратів відхилень в табл. 8.9. (3115,16) дорівнює підсумку останньої графи табл. 8.7. На підставі цієї суми було визначено варіацію урожайності, зумовленої спільною дією двох факторів:

"¥п+д = 681,18 з числом ступенів свободи кп+д = 5.

Ця сума квадратів відхилень складається із таких складових компонентів:

Визначимо число ступенів свободи варіації для кожної з обчислених сум квадратів відхилень. Для цього необхідно ступені свободи варіації двох факторів (кп+д = 5) розподілити між трьома компонентами, що складають цю суму квадратів відхилень (кп, кд і кю):

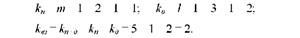
Об'єднаємо результати обчислень двох етапів, розрахуємо і проаналізуємо дисперсії (табл. 8.10).

Таблиця 8.10. Розрахунок і аналіз дисперсій

розрахунок і аналіз дисперсій

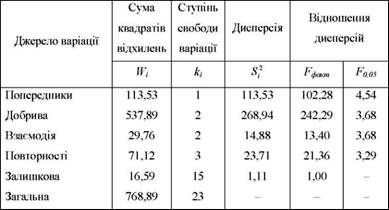
Фактичне дисперсійне відношення знайдемо за формулою

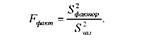
О2 . п2

Наприклад, по добривах становитиме д o = 268,94 : 1,11 =

242,29, по взаємодії факторів евз : езад = 14,88 : 1,11= 13,40 і т. д. Табличні значення Б при рівні значущості а = 0,05 визначимо за додатком 4 для оцінки відношення дисперсії попередників до дисперсії залишкової - на перетині 1-го стовпця і 15-го рядка (Б005 =4,54); для відношення дисперсії добрив до дисперсії залишкової - 2-го стовпця і 15-го рядка (Б005 = 3,68) і т. д.

Порівняння фактичних і табличних значень Б-критерію Фішера при заданому рівні значущості а = 0,05 показує, що в усіх випадках Тфщт > Б005.

Отже, висунуті нульові гіпотези не узгоджуються з фактичними даними і тому їх потрібно відхилити. Відмінності в урожайності за факторами і повторностями є істотними, вірогідними, вірогідним є проявлення ефекту взаємодії факторів.

Оскільки за результатами дисперсійного аналізу нульові гіпотези відхилено і доведено істотність відмінностей між середніми, можна оцінити вірогідність різниць між парами середніх. Для цього потрібно обчислити середню і можливу граничну помилку вибірок (Єр) і аналогічно тому, як це було зроблено в попередньому прикладі, знайти фактичні різниці між парами середніх і порівняти їх з можливими граничними різницями (НІР).

Схожі статті




Теорія статистики - Мармоза А. Т. - 8.4. Дисперсійний аналіз при групуванні даних за двома ознаками

Предыдущая | Следующая