Теорія статистики - Мармоза А. Т. - 8.3. Застосування дисперсійного аналізу для оцінки вірогідності різниці двох середніх

Критерій Б дозволяє встановити наявність або відсутність істотних зв'язків між груповими середніми в цілому, однак він не показує, між якими середніми різниця істотна, а між якими неістотна.

Тому, якщо проведений дисперсійний аналіз призвів до відмови від нульової гіпотези, що передбачає рівність середніх, та показав істотність впливу перевіряємого фактора на результативну ознаку, то цей загальний висновок може бути конкретизований, доповнений перевіркою істотності відмінностей між парами середніх.

Для перевірки нульової гіпотези про вірогідність відмінностей між парами середніх використовується ряд методик і критеріїв.

Для випадку, коли чисельності вибірок (груп) між собою рівні (п1 = п2 =...=пк) і групування проведене за якісною ознакою, найточніша оцінка вірогідності відмінностей між середніми може бути здійснена при використанні методики Хартлі. В свою чергу, ця методика грунтується на використанні 0_-критерію Тьюкі. При нерівних чисельностях вибірок доцільно застосовувати метод контрастів Шеффе. При невеликій кількості варіантів досліду (не більше трьох) можливе використання.- критерію Стьюдента. При багатоваріантному досліді (більше трьох) застосування цього критерію дає збільшену кількість вірогідних зв'язків.

Методика застосування 0_-критерію Тьюкі така:

1) будують ранжирований ряд групових середніх;

2) визначають попарні різниці між середніми, спочатку між середніми, що стоять поряд, потім між середніми, віддаленими одна від одної на дві, три позиції і т. д.;

3) обчислюють фактичне значення 0_-критерію Тьюкі як відношення знайдених різниць до середньої помилки вибірки:

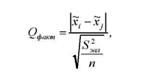
Де О32ая - дисперсія, обчислена у дисперсійному аналізі, П - кількість спостережень у кожному варіанті досліду (кількість повторностей);

4) визначають табличне значення (- критерію Тьюкі (дод. 7); при цьому значення 0_а різні для середніх, віддалених одна від одної на одну, дві, три позиції і т. д. і залежать від рівня значущості (його треба взяти таким самим, як і в дисперсійному аналізі), числа ступенів свободи і порядку різниць І ( І = 2 для сусідніх в ранжированому ряду середніх, І = 3 для середніх, які відстоять одна від одної на дві позиції і т. д.);

5) зіставляють (факт і 0_а; якщо (факт > 0_а, то нульову гіпотезу про рівність двох середніх відхиляють, а різницю між середніми вважають істотною (вірогідною), якщо ж (факт < (((а, то нульову гіпотезу приймають, а різницю між середніми визнають неістотною оскільки, вона знаходиться в межах можливих випадкових коливань.

Вірогідність різниці між парами середніх може бути оцінена також шляхом співставлення її з гранично можливою помилкою вибірки Є. р, яка вказує межі граничних випадкових коливань і дістала назву Найменшої істотної різниці (НІР). Можлива гранична помилка при використанні Г-критерію Стьюдента розраховується за формулою ер = Г Д_2, при використанні більш строгого (-критерію Тьюкі - за формулою £Р = С( Д-2.

Якщо різниця між двома порівнюваними середніми, більша за абсолютною величиною, ніж можлива гранична помилка (НІР), то роблять висновок про істотність різниці цих двох середніх. Якщо ж можлива гранична помилка буде більшою від фактичної різниці, то різниця між двома середніми лежить у межах можливих випадкових коливань, тобто вона є невірогідною.

Проведемо оцінку істотності різниці між парами середніх по розглянутому прикладу, оскільки був одержаний загальний висновок щодо вірогідності впливу раціонів на прирости живої маси бройлерів.

Нагадаємо, що за даними досліду, що аналізується, вже розраховані три групові середні (табл. 8.1): х1 = 32; *2 = 34; х3 = 39 (г). Залишкова дисперсія,

Обчислена в дисперсійному аналізі, становила S^aя =1,91, їй відповідало число ступенів свободи кзал = 8, кількість повторностей П = 5.

Сформулюємо Н0 і На. За даними досліду можливі такі три порівняння:

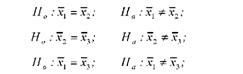
Рівень значущості а = 0,05. Найбільш потужним критерієм перевірки Н0 такого роду є О-критерій Тьюкі.

Для перевірки Но необхідно розрахувати фактичні значення критерію Офакг і порівняти їх з табличними значеннями О_0)05.

Побудуємо ранжирований ряд групових середніх за величиною середніх приростів живої маси (г):

Визначимо середню помилку вибірок:

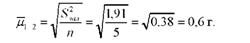
Обчислимо фактичне значення О-критерію Тьюкі для кожної пари середніх:

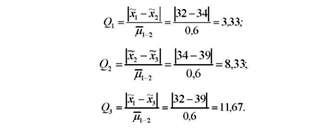
Встановимо критичні значення 0_-критерію Тьюкі (дод. 7) при а = 0,05; для різниць першого (/ = 2) порядку Од05 = 3,261; для різниць другого (/ = 3) порядку О_005 = 4,041. Порівняємо фактичні і табличні значення 0_-критерію (табл. 8.4).

Таблиця 8.4. Дані для аналізу статистичної оцінки різниці між парами середніх

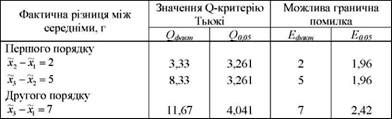
дані для аналізу статистичної оцінки різниці між парами середніх

Оскільки для всіх трьох порівнянь (факт > О^ю, нульові гіпотези про рівність середніх в генеральних сукупностях відхиляються.

Ті самі висновки матимемо, порівнюючи можливу граничну помилку (НІР) з фактичною різницею між парами середніх.

Визначимо £р:

А) для різниць першого порядку

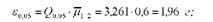
Б) для різниць другого порядку

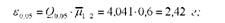
Можлива гранична помилка (НІР) показує, що внаслідок випадкового варіювання різниця між парами середніх першого порядку може досягати 1,96 г, другого порядку - 2,42 г.

Порівняння фактичних і гранично можливих значень різниць між парами середніх (табл. 8.4) показує, що всі три фактичні різниці перевищують межі можливих випадкових коливань.

Отже, з імовірністю помилки тільки в 5 випадках із 100 можна стверджувати, що різні за якістю раціони істотно впливають на прирости живої маси бройлерів.

Схожі статті




Теорія статистики - Мармоза А. Т. - 8.3. Застосування дисперсійного аналізу для оцінки вірогідності різниці двох середніх

Предыдущая | Следующая