Теорія статистики - Мармоза А. Т. - Середня квадратична

Середню геометричну застосовують, коли загальний обсяг явища є не сума, а добуток значень ознаки. Ця середня використовується здебільшого для розрахунку середніх коефіцієнтів (темпів) зростання і приросту при вивченні динаміки явищ (див. розділ 10) і має такий вигляд:

Де п - число коефіцієнтів зростання; у і у - початковий і кінцевий рівні динамічного ряду.

Величина середньої геометричної залежить тільки від співвідношення кінцевого і початкового рівнів. Якби не змінювались в цих межах інші рівні, величина середньої не зміниться.

Розглянемо такий приклад. За даними про посівну площу цукрових буряків у господарстві за 5 років знайти середній коефіцієнт зростання площі посіву цукрових буряків за 2005 - 2009 рр. Всі розрахунки зведемо в табл. 4.5.

Таблиця 4.5. Дані для розрахунку середньої геометричної

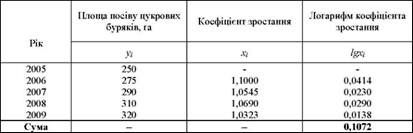
дані для розрахунку середньої геометричної

Середнє значення логарифма коефіцієнта зростання становитиме: 0,1072 : 4 = 0,0268. За таблицями антилогарифмів знайдемо середній коефіцієнт зростання посівної площі цукрових буряків: Апіії%х = 1,0636, або 106,36%.

Такий саме результат одержимо і за другою формулою:

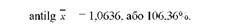
Отже, середній коефіцієнт зростання посівної площі цукрових буряків у господарстві за 2005 - 2009 рр. становив 1,0636. Інакше кажучи, посівна площа цукрових буряків у господарстві щорічно збільшувалась в середньому на 6,36%.

Середня квадратична

Середня квадратична використовується переважно для розрахунку показників варіації (коливання) ознаки - дисперсії і середнього квадратичного відхилення, які обчислюються на основі квадратів відхилень індивідуальних значень ознаки від їхньої середньої арифметичної. Крім того, вона застосовується для узагальнення ознак, виражених лінійними мірами яких-небудь площ (при обчисленні середніх діаметрів стовбурів дерев, кошиків, листків, клубнів тощо).

Формули її такі:

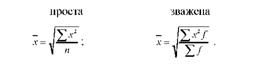
Наприклад, є дані про розмір діаметрів стовбурів трьох яблунь (Хг ): 17; 22; 19 см. Потрібно обчислити середній розмір діаметра стовбура яблуні. Оскільки вихідні дані представлені у вигляді квадратних функцій, середній розмір діаметра стовбура яблуні визначимо за формулою середньої квадратичної простої:

Якби у наведеному прикладі окремі значення діаметра стовбура повторювались неоднакове число разів, то середній розмір діаметра стовбура слід було б розраховувати за формулою середньої квадратичної зваженої.

Досліджуючи статистичну сукупність, можна виявити, що поряд з ознаками, які притаманні усім одиницям досліджуваного явища, є й такі ознаки, якими одні одиниці володіють, а інші ні. Такими ознаками, наприклад, будуть наявність в партії продукції бракованої продукції, рослини уражені хворобами та ін. Такі виключаючі один одного ознаки називають Альтернативними. При альтернативній варіації, коли є лише два виключаючих один одного випадки, наявність ознаки у одиниці сукупності прийнято позначати 1, а її відсутність - 0. Частку одиниць, що володіють досліджуваною ознакою, позначають р, а долю одиниць, не вододіючих цією ознакою, - Д. Очевидно, що Р + д = 1, а д = 1 - р.

Середнє значення альтернативної ознаки, обчислене за формулою середньої арифметичної, буде дорівнювати:

Отже, середнє значення альтернативної ознаки дорівнює частці одиниць сукупності, що володіють даною ознакою.

Якщо обчислити різні типи середніх величин, одержаних з степеневої середньої, для одного і того самого варіаційного ряду, то їх чисельні значення будуть відрізнятися один від одного, а самі середні розташуються таким чином:

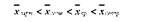
Тобто найбільшою буде середня квадратична, а найменшою - середня гармонічна. Порядок зростання середніх визначається значенням степені К в степеневій середній.

Ця властивість степеневих середніх одержала назву властивості мажоРАнтності сеРЕдніх.

Приклад. Нехай маємо такі значення ж,: 2; 3; 36. Обчислимо вказані середні величини:

Одержані середні розташуються у такому порядку: 3,50 <6,00< 13,67< 20,89, що відповідає вимозі властивості мажорантності середніх:

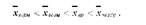
Схожі статті




Теорія статистики - Мармоза А. Т. - Середня квадратична

Предыдущая | Следующая