Теорія статистики - Мармоза А. Т. - Розподіл Стьюдента

Теоретичні положення по оцінці вибіркових характеристик на основі малих вибірок (п < 30) вперше (1908 р.) розробив англійський математик-статистик В. Госсет (що друкував свої роботи під псевдонімом Стьюдент). Пізніше (1925 р.) Р. Фішер дав більш строге доведення цього розподілу, яке дістало назву І - Розподілу Стьюдента.

Відхилення вибіркових середніх від генеральної середньої Стьюдент виразив в одиницях стандартного відхилення

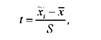
Де в знаменнику використовується середнє квадратичне відхилення вибірки, тоді як в нормальному розподілі - середнє квадратичне відхилення генеральної сукупності (сто). Р. Фішер виразив ці відхилення в одиницях стандартної помилки

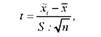
_ _5_

Де ~ - середня помилка в малих вибірках.

Середнє квадратичне відхилення в малих вибірках визначається з врахуванням числа ступенів свободи варіації (п - 1):

Теоретичний і-розподіл Стьюдента не залежить від параметрів генеральної сукупності, він пов'язаний тільки з величинами, що визначаються безпосередньо за даними вибірки.

В літературі з математичної статистики доводиться, що диференціальна функція І - розподілу Стьюдента (щільність розподілу імовірностей) має вигляд

Де А - величина, яка визначається з врахуванням числа ступенів свободи варіації (к = П - 1) за допомогою гамма-функції (Г - функції):

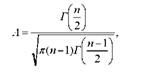
Де Г(п) |х е сіх - Гамма-функція.

0

Як видно, величина А Залежить тільки від обсягу вибірки і відповідає максимальній ординаті кривої розподілу при і = 0. Імовірність того, що помилка вибірки буде не більше заданої величини Єр = іМ Визначається інтегральною функцією

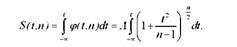
Інакше кажучи, П) = Р(іТабл < іФакг), Де іТабл І іФакг - табличне (теоретичне) і фактичне значення нормованого відхилення.

І-розподіл Стьюдента справедливий тільки для вибірок, взятих із генеральної сукупності з нормальним розподілом випадкової величини.

На рис. 6.2. порівнюється крива і-розподілу Стьюдента з кривою нормального розподілу.

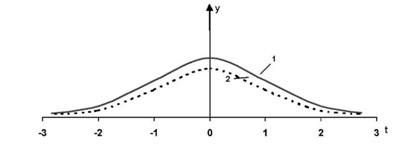
порівняння і - розподілу стьюдента і нормального розподілу

Рис. 2.2. Порівняння і - Розподілу Стьюдента і нормального розподілу: 1 - нормальний розподіл; 2 - і-розподіл Стьюдента

Крива T - розподілу Стьюдента симетрична відносно осі ординат. На відміну від нормального розподілу під кінцями кривої t - розподілу Стьюдента при тих самих значеннях t розміщена значно більша частина площі. Таким чином, на частку більших відхилень від генеральної середньої припадає значна частина площі. Це означає, що для малих вибірок імовірність допущення більших помилок суттєво підвищується.

При збільшенні обсягу вибірки T - розподіл Стьюдента наближається до нормального розподілу (практично вважається достатнім И > 30), а при и^<ю він стає нормальним.

Для визначення значень функції S(t, и) розподілу Стьюдента складено ряд спеціальних таблиць, в яких наводяться розрахункові значення S(t, и) при відповідному числі ступенів свободи варіації. За цими таблицями можна знайти імовірність помилки вибірки при заданому значенні нормованого відхилення t або значення T при заданому рівні імовірності судження Р.

Наведемо витяг з таблиці імовірностей S(t, и) для значень nit, які найбільш часто застосовуються (табл. 6.2).

Таблиця 6.2. Витяг з таблиці значень функції S (t, N) розподілу Стьюдента (імовірності помножені на 1000)

И

T

4

5

6

7

8

9

10

12

15

20

00

1

608

626

636

644

650

654

656

662

666

670

683

2

860

884

902

908

914

920

924

930

936

940

954

3

942

960

970

976

980

984

984

988

992

992

997

Як видно з даних таблиці, імовірність розходження між вибірковою середньою малої вибірки і генеральною середньою залежить від двох величин: чисельності вибірки П і нормованого відхилення і. Можна побачити, що при збільшенні П цей розподіл прямує до нормального і при п = 20 вже мало від нього відрізняється. При п^<ю в таблиці наведені значення для функції нормального розподілу.

Інший аспект застосування розподілу Стьюдента наведений в додатку 3, в якому дані значення і - критерію Стьюдента при різному рівні значущості (а) і числі ступенів свободи варіації (к).

Розподіл Пірсона

Для оцінки розходжень між емпіричними і теоретичними частотами розроблено ряд критеріїв згоди, серед яких найбільш широке застосування отримав критерій %г - хі-квадрат. На основі зіставлення фактичного і теоретичного (табличного) значення %г - критерію можна вияснити належність даного емпіричного розподілу деякому відомому теоретичному типу розподілу (наприклад, є або ні досліджуваний розподіл нормальним, біноміальним та ін.).

Крива, що характеризує розподіл %г описується рівнянням

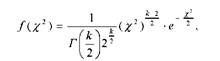
Де К- число ступенів свободи варіації.

Враховуючи, що для цілих додатних чисел гамма-функція Г(п) = п - 1, можна записати

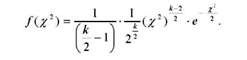
З рівняння щільності імовірності видно, що розподіл х 2 залежить тільки від числа ступенів свободи варіації (к = п - 1). Розподіл %г не залежить від генеральної середньої і генеральної дисперсії. При великій чисельності вибірки (при П = 30 - 40) розподіл %г практично стає нормальним.

Для %г критерію складені спеціальні таблиці, в яких наведені його значення при певному числі ступенів свободи варіації і заданому рівні імовірності (дод. 6).

Викладення аспектів прикладного застосування %г - критерію дається в розділі, присвяченому питанням перевірки статистичних гіпотез (розділ 7).

Розподіл Фішера-Снедекора

При розв'язуванні ряду задач кореляційно-регресійного і дисперсійного аналізу використовується розподіл Е, названий так по першій літері прізвища англійського математика-статистика Р. Фішера.

Якщо И І V- незалежні випадкові величини, розподілені за законом %г з ступенями свободи К1 і к2, То величина

Підпорядковується розподілу Е Фішера-Снедекора з ступенями свободи К1 І К2. Приймаючи, що И > V, величина Е Буде мати значення не менше одиниці. Щільність розподілу Е має вигляд

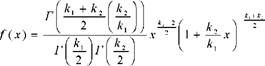
З формули видно, що розподіл Е Визначається двома параметрами, тобто числами ступенів свободи варіації к1 і к2. Це дає змогу скласти таблиці розподілу випадкової величини Е, в яких різним значенням рівня значущості і різним сполученням величин к1 і к2 відповідають певні значення Е-критерію (дод. 4 і 5).

Використання Е-критерію в статистичному аналізі детально розглянуто в розділі 8 "Дисперсійний аналіз".

Схожі статті




Теорія статистики - Мармоза А. Т. - Розподіл Стьюдента

Предыдущая | Следующая