Статистика - Опря А. Т. - § 10.3. Система індексів для характеристики динаміки складного явища

Із розглянутого вище зрозуміло, що явища, динаміка яких вимірюється індексами, складаються з різнорідних елементів. Це зумовлює неможливість вимірювання рівнів таких явищ. Із цього випливає необхідність їх вимірювання в динамічному розрізі. Тому при обчисленні індексу завжди мають справу з двома рядами величин, які характеризують базисний і поточний періоди.

Залежно від періоду часу, який береться за основу при побудові індексів, останні можуть бути базисними та ланцюговими. Базисними називають індекси, які мають один і той самий період часу, взятий за основу розрахунків, тобто постійну базу порівняння. Наприклад, якщо при розрахунках індексів за 2001 - 2004 рр. за базу порівняння взяти 2001 р., то такі індекси називатимуться базисними. Якщо ж при обчисленні індексів база порівняння змінюватиметься і за таку базу братимуть період, який є попереднім щодо обчислюваного індексу, то останній називатиметься ланцюговим. Як базисний, так і ланцюговий індекси дають кількісну характеристику темпів розвитку явища.

Розглянемо приклад (табл.75). При обчисленні базисних індексів за базу порівняння прийнято 2001 р. Останній рядок таблиці показує: а) по графі базисних індексів - в 2004 р. порівняно з 2001 - м середня врожайність збільшилася на 1,5 % (індекс 1,015) ; б) по графі ланцюгових індексів - в 2004 р. порівняно з 1994 - м середня урожайність зменшилась на 1,8 % (індекс 0,982).

Між базисними і ланцюговими індексами існує певний взаємозв'язок: добуток ланцюгових індексів дорівнює базисному індексу останнього періоду 1,018><1,015х0,982х=1,015.

Таблиця 75

Динаміка врожайності зернових культур у господарстві_

Рік

Урожайність, ц/га

Індекси

Базисні

Ланцюгові

2001

33,1

-

-

2002

33,7

1,018

1,018

2003

34,2

1,033

1,015

2004

33,6

1,015

0,982

Щоб довести правильність цього рівняння, перемножимо ті дроби, на підставі яких були обчислені ланцюгові індекси, та здійснимо відповідні скорочення:

33,7 34,2 33,6 Іт, - х-х-= 1,015

33,1 33,7 34,2 .

Отже, одержано базисний індекс 2004р. У результаті скорочення залишаються лише знаменник першої ланки і чисельник останньої,

. . 1 = - М = 1,015

Що дає тотожність з базисним індексом : 33,1 .

Зазначена взаємозалежність на прикладі індивідуальних індексів поширюється і на співвідношення агрегатних. Але таке співвідношення має місце за умови, що зважування, здійснюється лише постійними сумірниками (вагами)наприклад, базисного періоду.

Розглянемо зазначену залежність на прикладі співвідношення індексів фізичного обсягу:

Як бачимо, знаменник другої ланки скорочується з чисельником першої, знаменник третьої ланки - із чисельником другої і залишаються чисельник третьої ланки та знаменник першої, що тотожне базисному індексу.

Слід відзначити, що при інтерпретації індексів, якими вимірюють динаміку явищ, іноді застосовують термін "пункт". Під останнім розуміють одиницю, якщо база порівняння при обчисленні індексу виражена у вигляді 100 %. Наприклад, якщо індекс обсягу виробництва продукції підвищився з 125 % у 2003 р. до 135 % у 2004 - му при базі порівняння 2000 р. 100 %, то можна сказати, що індекс збільшився на 10 пунктів.

Індекси з постійними і змінними вагами. Як уже згадувалося, взаємозв'язок між базисними і ланцюговими індексами (добуток ланцюгових дорівнює базисному) є безумовним лише для індивідуальних індексів. Для загальних такий взаємозв'язок не порушується, якщо ряд загальних індексів розраховано з постійною вагою.

Приклад. Маємо дані по підприємству про виробництво продукції та про Ціни на неї за чотири роки:___

2001

2002

2003 2004

Я1/Р1

Я2/Р2

Я3/Р3

Я4/Р4

При обчисленні базисних і ланцюгових індексів фізичного обсягу можна по-різному вирішити питання про еліміновані величини (ваги). Так, при визначенні ланцюгових індексів фізичного обсягу продукцію всіх періодів можна оцінити в одних і тих самих цінах (наприклад, у цінах 2001 р.) такі індекси мають вигляд:

Т __ЕЯ2Р1 Т _И, Я3Р1 Т _Х/иРр_

^2/1 V - Т3/2 V - Т4/3 ^

X Я1Р1 ; X Я2Р1 ; X Я3Р1

Оскільки розраховані таким чином індекси мають однакові ваги (р1) , то представляють ряд індексів з постійними вагами. У цьому випадку можна перейти від ланцюгових індексів до базисного (і навпаки):

X Я2 Р1 X Я3Р1 X Я4 Р1 = X Я4Р1 X Я1Р1 И, Я2Р1 X Я3Р1 X Я1Р1 .

Але при побудові ряду ланцюгових індексів можна було б піти іншим шляхом : для кожного періоду побудувати індекс фізичного обсягу за цінами попереднього періоду:

Т _ XЯ2Р1 Т _ XЯ3Р2 Т _Х/І4Р3_ X Я1Р1 ; X Я2Р2 ; XЯ3Р3

Ці індекси побудовані за різними вимірниками (вагами), тобто вони є Індексами зі змінними вагами. Для таких індексів перехід від ланцюгових до базисних (і навпаки) неможливий.

Відзначаючи позитивну особливість індексів із постійними вагами, що зумовлює перехід від ланцюгових індексів до базисних (і навпаки), слід вказати й на недоліки деяких видів економічних індексів. Так, чи можна вважати доцільною побудову індексів цін із постійними вагами? І дійсно, який сенс розрахунку індексу цін у четвертому періоді (порівняно з третім) за продукцією першого періоду (я1)? З практичного боку для цін значно більший інтерес становлять індекси зі змінними вагами, хоча їм і не притаманна вказана вище взаємозалежність між ланцюговими та базисними індексами.

Індекси змінного і постійного складу. У розглянутих вище прикладах йшлося про випадки, коли для сукупності невимірних показників у натуральному вигляді визначалася середня зміна індексованих величин. При вивченні динаміки якісних показників часто треба визначати зміну середньої величини індексованого показника для будь - якої однорідної сукупності (наприклад, середньої врожайності, середньої трудоємності надою, середньої собівартості і т. д.).

У загальному вигляді динаміку таких середніх показників можна представити виразом (хі :х0), який являє собою середній індекс.

Відносну величину, що характеризує динаміку двох середніх показників для однорідної сукупності, в статистиці називають індексом змінного складу.

Для якісних показників, наприклад урожайності і цін, індекси змінного складу легко записати у вигляді таких відношень:

' Уп ' Уп '

Назва індексу змінного складу зумовлена тим, що середні величини, динаміку яких вони відображують, можуть змінюватися залежно від змін кожної окремої одиниці досліджуваного явища та від змін його структури. Наприклад, збільшення середньої врожайності зернових культур залежить від підвищення врожайності кожної окремої культури (вівса, ячменю, гречки і т. д.) та від збільшення питомої ваги в загальній площі зернових найбільш урожайних культур.

Таким чином, індекс змінного складу характеризує спільний вплив зазначених вище факторів. У такому індексі знаходить прояв зміна обох величин - кількісних (П0, П1) т а якісних (у0 і У1).

У загальному вигляді формула індексу змінного складу така: Т У Х1/1 У ■"*0/0 -

Де Х - осереднювана ознака ; ї - вага (питома вага) досліджуваного явища.

Якщо дослідження має на меті виключити вплив змін структури сукупності на динаміку середніх показників розраховують середні для двох періодів по одній і тій самій структурі, що, як правило, фіксується по звітному періоду. Індекс, який відображує динаміку середніх величин при фіксованій структурі явища, називається Індексом постійного (фіксованого ) складу. Він характеризує вплив лише індексованої величини. Його структурна формула має вигляд:

І = Е Х1/1: ЕХ0/1

Л/1 Л/1 або

І =_Е91Р1 Т, 90Р1

2291 ' 2291

При скороченні в наведеній формулі на Еї1 одержуємо вже відому формулу агрегатного індексу : 1 ~ т^ : 22.

У даному індексі вплив структурного фактора виключено. Прикладом таких індексів є індекси фізичного обсягу (£90Р°), індекси цін ( £), індекси собівартості ( Е2^1) та ін.

Відношенням індексів змінного складу до індексу фіксованого

Складу одержують індекс структури : 1стр - ~ (£^ : ^-Л):(£■Х°/'0: X-ЛО,

Тобто 1стр. ~ 1флюі-: . Таким чином завжди можна обчислити один з індексів, якщо відомі два інших. Даний індекс характеризує Вплив змін структури на зміну середньої величини.

Таблиця 76

Вихідні і розрахункові дані для обчислення індексів змінного та Фіксованого скла/ту

Культура

Площа, га

Урожайність, ц/га

Валовий збір, ц

Базисний період

Звітний період

Базисний період

Звітний період

Базисний період

Звітний період

Умовний

П0

П1

У0

>1

Л П0

У1 ГІ1

У0 П1

Пшениця

500

590

30

35

15000

20650

17700

Жито

200

250

12

15

2400

3750

3000

Разом

700

840

-

-

17400

24400

20700

Приклад. Розглянемо розрахунку зазначених вище індексів за даними таблиці 76. Середня врожайність базисного і звітного періодів становить:

- =ХУЛ = і7400 = 24,9; " = ІА = 24440 = 29,0 X П0 700 1 X Д1 840

Обчислимо індекси врожайності змінного і постійного складу та їх співвідношення:

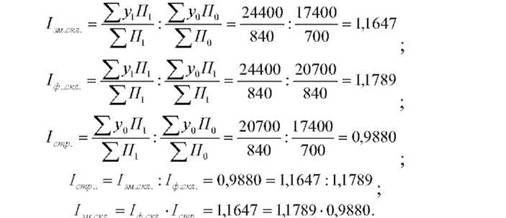
Прокоментуємо результати розрахунків. Індекс урожайності змінного складу відображує динаміку середньої врожайності. У нашому випадку середня

Врожайність зернових культур підвищилася на 16,5 % як за рахунок збільшення врожайності окремих культур, так і за рахунок змін структури посівних площ. Перш ніж визначити вплив на динаміку врожайності змін структури посівних

Площ (^ч"--), розраховують індекс урожайності фіксованого складу (^#-™). Він виключає вплив структури посівних площ. Індекс дорівнює 1,1789 і показує, що середня врожайність у звітному періоді порівняно з базисним підвищилася на 17,9 % за рахунок зростання врожайності окремих культур.

Розбіжність в індексах змінного та постійного складу можна пояснити впливом змін структури посівних площ. Величина індексу структури 0,988 свідчить про те, що зменшення питомої ваги високоврожайних культур у звітному періоді (пшениці - від 71 до 70 %) зумовило деяке зниження показника середньої врожайності (на 1,2 %).

Аналогічно можна розрахувати індекси змінного та фіксованого складу і для інших якісних показників у випадках, коли йдеться про сукупності, для яких розраховується середня величина індексованого показника (наприклад, для показників цін, собівартості, продуктивності праці і т. д.).

Схожі статті




Статистика - Опря А. Т. - § 10.3. Система індексів для характеристики динаміки складного явища

Предыдущая | Следующая