Статистика - Опря А. Т. - 6.2.5. Розподіл Фішера - Снедекора

При перевірці статистичних гіпотез розглядаються питання про критерії узгодженості. Останні дозволяють вирішити задачу про відповідність або невідповідність певного закону розподілу, обраного для відображення досліджуваного емпіричного ряду розподілу.

Розраховані критерії згоди зумовлюють можливість (або неможливість) прийняття для досліджуваного ряду розподілу моделі, яка виражається деяким теоретичним законам розподілу. Та чи інша модель розподілу що відповідає визначеному закону може бути прийнята шляхом порівняння графічних зображень. Вченими-математиками розроблено ряд критеріїв узгодженості, обчислення яких дозволяє дати кількісну оцінку наближеності емпіричних і теоретичних розподілів. Окремі з них оцінюють імовірність розходження фактичного і теоретичного розподілу, а деякі дають пряму відповідь про можливість відображення досліджуваного емпіричного розподілу обраним теоретичним законом.

Для характеристики (оцінки) розходження емпіричних і теоретичних частот англійським статистиком Карлом Пірсоном (1900) розроблено критерій узгодженості, так званий "хі - квадрат". Даний критерій застосовується в тих випадках, коли необхідно визначити ступінь відмінності фактичного розподілу частот від теоретичного.

Теоретичний аспект визначення хі - квадрата як критерію може бути зведений до таких міркувань.

Якщо у вибірку з генеральної сукупності, розподіленої за нормальним законом (^^ХП), ввести центровані і нормовані

Х - X

" - o o

Величини ( Ст ) і підсумовувати їх квадрати, одержимо значення

2 ■

Величини "хі - квадрат" (% ) '

^2 _ (Х1 ~ Х)2 + (-*2 ~ Х)2 + Х3 ~ Х)2 + + ( ХП ~ Х)2 _ £ ( ХІ ~ Х)2

А а а а 1=1 А

У даному випадку величина Х, яка зумовлюється дисперсією °2 розподіляється за законом:

1 ^

І(XІ) = И И (Ж2) 2 е 2,

2-Г (-) 2 2

... . Д-) .

Де і) - число ступенів вільності, яке дорівнює п-1 ; 2 - гама-функція,

Зокрема Г(п+1)=п.

Як видно з наведеного вище виразу, розподіл "хі - квадрат" визначається одним параметром - числом ступенів вільності.

Для різних обсягів вибірки (точніше - значень числа ступенів вільності) розподіл величини "хі - квадрат" буде асиметричним. При цьому, чим менша вибірка, тим сильніше проявляється асиметрія. Із збільшенням чисельності вибіркової сукупності асиметрія зменшується і розподіл "хі - квадрат" переходить у нормальний. Наочно характер такої зміни ілюструє графік (рис. 18).

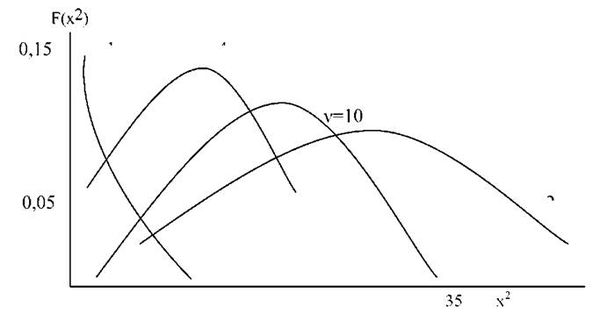
Рис. 18. гозподіл ("хі - квадрат" при різних значеннях числа ступенів вільності

Якщо прийняти рід емпіричних і теоретичних частот відповідно за П - і Пп, обчислення "хі - квадрат" - критерію виразиться формулою:

Судячи по параметрах формули, величина критерію Пірсона являє собою суму відношень між квадратами різниць емпіричних і теоретичних частот до теоретичних частот.

Інтегрування диференціальної функції розподілу (за її складності) являє певні обчислювальні утруднення. У зв'язку з цим Р. Фішером розроблено стандартні математичні таблиці розподілу "хі - квадрат" (додатки 6, 7). Ці таблиці дають змогу обчислити ймовірність того, що випадкова величина, яка підпорядковується закону розподілу "хі - квадрат" з певним числом ступенів вільності,

Перевищить деяке фіксоване значення Х* , або Р(х

Другий аспект використання названих стандартних таблиць полягає у тому, що за їх допомогою можна встановити критичне значення "хі - квадрата", перевищення якого для відомого числа ступенів вільності буде свідчити про невідповідність досліджуваного розподілу нормальному закону. Є й інші аспекти практичного використання "хі - квадрат" - критерію. Розглянемо лише приклад для випадку встановлення ймовірності Р(х

Для вибірки з числом ступенів вільності і) =21, що підпорядковується

Закону "хі - квадрат" розподілу (% ) необхідно визначити відхилення Я*, імовірність перевищення якого дорівнює 0,05, тобто необхідно знайти "хі -

Квадрат" при і) = 21, для якого: ^21) = 0,05. Шукана Величина буде

Знаходитись (додаток 7) на перетині рядка 21 і графи 0,95 і Становитиме Ху =

32,7. Звідси маємо:Р(%2>32,7) = 0,05.

2

Таким чином, величина %У, імовірність перевищення якої 0,05, буде 32,7

Слід відзначити деякі неточності, що існують у навчальній літературі при викладі питань "хі - квадрат - критерію". Відносно його відкриття, крім дати 1900 р. (Пірсон), слід пам'ятати і дату 1876 р. (Хельмерт).

2

Що ж стосується стандартної таблиці Х. - розподілу, то буде неточним її інформацію називати "Критерій Персона", бо розробка цієї таблиці належить Р. Фішеру. Останній вважав замість значень ймовірностей Р% , що відповідають деякому ряду % , розраховувати значення Х, які відносяться до обраних рівнів імовірностей при різному числі ступенів вільності.

Ще одне зауваження щодо символіки написання "хі - квадрат".

2 2

Звичайно прийнята форма Х. Більш правильним буде Хт Але, якщо виключена можливість невірного розуміння, її можна записувати з одним підрядковим числом (індексом). Якщо це не заважає правильному сприйманню змістовного навантаження параметра, запис його може бути і без підрядкових індексів.

6.2.5. Розподіл Фішера - Снедекора

У цілому ряді задач, вирішуваних математичною статистикою,

Зокрема у дисперсійному і кореляційно - регресійному аналізі,

Використовується "розподіл Б", названий так по перший літері

Прізвища англійського статистика-математика Р. Фішера. Якщо И1 і

И2 незалежні випадкові величини з розподілами % , і з і ^

Ступенями вільності відповідно, то випадкова змінна. Б буде

... Я? : У, П уГ г = -1-1 = -- х-.

И : V И V дорівнювати: 2 ■ 2 2 1

Одержана величина називається випадковою змінною з

Розподілом Фішера-Снедекора з1^ та ^ ступенями вільності.

Приймаючи, що И1 ^2 величина Б буде мати лише значення, не

Менше як І.

Щільність імовірності випадкової змінної Б, яка має розподіл Фішера - Снедекора з ^ і ^ ступенями вільності, має вигляд:

Н(Р) =-2-У±-р 2 (1 + Р) 2

Внаслідок великої складності розрахунку інтегралів доведення тут не наводиться. Але, як видно, розподіл Б зумовлений і визначається двома параметрами, тобто числами ступенів вільності ^ і У2. Розподіл випадкової змінної Б подано у вигляді спеціальних математичних таблиць. Останні побудовані так, щоб для різних рівнів довірчої ймовірності (в основному для Р = 0,95; Р = 0,99, Р = 0,999) і для різних сполучень числа ступенів вільності У1 і У2 даються значення Б. Якщо прийняти позначення розрахункової і табличної

Величини Б відповідно як Рр і РТ, то для них справедлива буде рівністьР^Р^Рт}~А; Такі таблиці наведено в додатках 8, і 9. Практичне їх використання буде розглянуто у розділах "Дисперсійний аналіз"; "Кореляційно - регресійний аналіз"; "Методи багатомірного статистичного аналізу". Тут наведемо лише схематичний приклад.

Приклад. Вивчивши кількісний вплив фактора рівня продуктивність праці на її оплату по вибірці 60 підприємств, одержані наступні характеристики:

Факторна дисперсія *~ 3,06, залишкова дисперсія АГ = 0,15. Число ступенів

Вільності для факторної ознаки У* = 3 - I =2; для неврахованих факторів 60 -

3 = 57.

Розрахункова величина і - критерію становитиме: 0.15 .

За стандартною таблицею Р - розподілу знаходимо для рівня ймовірності

Р =0,95 і ступенів вільності У1=2.і ^ = 57 табличне значення РТ = 3,15 ; РР>ТГ (20.4 >3,15).

Знайдені параметри свідчать про те, що в досліджуваних підприємствах вплив рівня продуктивність праці на її оплату виявився вірогідним із рівнем імовірності 0,95.

На закінчення відзначимо, чому розподіл і називають розподілом Фішера - Снедекора. Справа в тому, що Р. Фішер перший дослідив розподіл відношень двох вибіркових дисперсій, але предметом його вивчення був розподіл не відношень дисперсій, а

Логарифмічної величини 2 °2 Дещо пізніше американський

Статистик Дж. Снедекор розрахував таблиці розподілу змінної ( °2) , що виявилося значно зручніше для практичного використання в розрахунках. Цей розподіл він назвав на честь Фішера "Розподілом Р". Пізніше даний вид розподілу почали називати "Розподілом Фішера-Снедекора".

Схожі статті




Статистика - Опря А. Т. - 6.2.5. Розподіл Фішера - Снедекора

Предыдущая | Следующая