Статистика - Опря А. Т. - 7.1.2. Алгоритми рішення дисперсійних моделей

Приклад. Розглянемо послідовність розрахунку однофакторного дисперсійного комплексу на прикладі залежності середньорічного надою корів ( V) від рівня годівлі (А) в 30 (п) підприємствах.

На першому етапі здійснюється групування підприємств за факторною ознакою. У даному прикладі сукупність підприємствах. поділена на три групи за рівнем використання кормів на корову в рік (А). Обробка вихідної інформації здійснюється за схемою таблиці 47.

С С

На підставі даних таблиці 47 знаходимо загальну ( У), факторну ( *), залишкову (^ ) дисперсії:

С =УУ2 -^'= 39740 - 39138 = 602; п

(У V )2

СХ =У Н -^'= 39433 - 39138 = 295; п

СГ = 2 - XН = 39740 - 39433 = 307.

С с с

Співвідношення складових дисперсій ( " 2) до загальної ( У) показує ступінь участі факторних ознак у формуванні загальної їзмінюваності результативної ознаки. Так, ступінь впливу рівня годівлі корів на їх

^ = <к = 295 = 0,49 С 602

Продуктивність становитиме: У (49%).

Ступінь впливу суми інших неврахованих факторів на результативну

^ = 307 = 0,51 ' С 602

Ознаку обчислюється за таким співвідношенням: У ( 51%).

Таким чином, у розглянутому прикладі факторна ознака (рівень годівлі) визначає 49% загальної варіації результативної ознаки (надою).

Таблиця 47

Вихідні і розрахункові дані однофакторного дисперсійного комплексу

Дисперсія як показник різноманітності залежить від кількості одиниць спостереження (підприємств) у групі. Для визначення впливу факторів ця обставина не має значення. В інших же випадках, зокрема, при встановленні вірогідності впливу факторів, необхідний показник, вільний від вказаної залежності, що допускає порівняння груп, різних за кількістю елементів, що входять до них. Таким показником є коригована дисперсія - девіата.

Девіатою називають дисперсію, яка припадає на один елемент вільного варіювання або на один ступінь вільності.

■ ■ Г1

Корінь квадратний з девіати ° ) являє собою звичайний показник математичної статистики - середнє квадратичне відхилення

У нашому прикладі число ступенів вільності варіації (Г) для факторної

Ознаки і для неврахованих факторів становитиме відповідно : У* ~1 ~1 ~ 3 ~1 ~ 2; уГ= п -1 = 30 - 3 = 21, Де і - КІЛькІСть виділених груп; п - чисельність вибірки. Розрахуємо девіати :

Ст2 = ^ = 295 = 141,50; СТ2 = = 301 = 11,31

* у, 2 2 уГ 21

Критерієм вірогідності впливу факторної ознаки на результативну є співвідношення її девіати до девіати неврахованих факторів. Якщо розраховане співвідношення дорівнює чи більше визначеної стандартної величини, вплив вважається вірогідним з певним ступенем імовірності. Стандартні відношення девіат визначаються за спеціальними таблицями (додатки 8,9).

Знаходимо це співвідношення для факторної ознаки на такому прикладі:

= 4 = Н150 = 12,91. Р О 11,31

Одержаний критерій ( Р) порівнюємо з табличним його значенням при двох порогах ймовірності : 0,95; 0,99 (додатки 8,9).

Наведемо стандартні співвідношення девіат, що відповідають ступеням вільності варіації.

Імовірність Р Критерій Б

0,95 3,3

0,99 5,5

У нашому прикладі Р (12,91) > Гт (3,3). Отже, в досліджуваних підприємствах вплив рівня годівлі корів на їх продуктивність виявився досить сильним і вірогідним. Про вірогідність результатів аналізу свідчить високий ступінь імовірності 0,99.

Приклад. Розрахунок двофакторного дисперсійного комплексу розглянемо на прикладі вивчення залежності собівартості 1ц молока (V) в 30 підприємств району від рівня концентрації поголів'я корів (А) і спеціалізації виробництва молока (В). з цією метою сукупність розділена на 2 групи з подальшим поділом на 2 підгрупи (табл. 48).

С

На підставі розрахункових даних таблиці 48 визначаємо загальну ( '), факторну ( * ) і залишкову (^ ) дисперсії:

С =2>2 - 2£1 = 23328,61 - (826,98)2 = 532,14;

С, =2Н - ^ = 23023,33 - (826,98)2 = 226,80; С2 = УУ2 - ^Н = 23328,67 - 23023,33 = 305,34.

Таблиця 48

Вихідні і розрахункові дані двофакторного дисперсійного комплексу

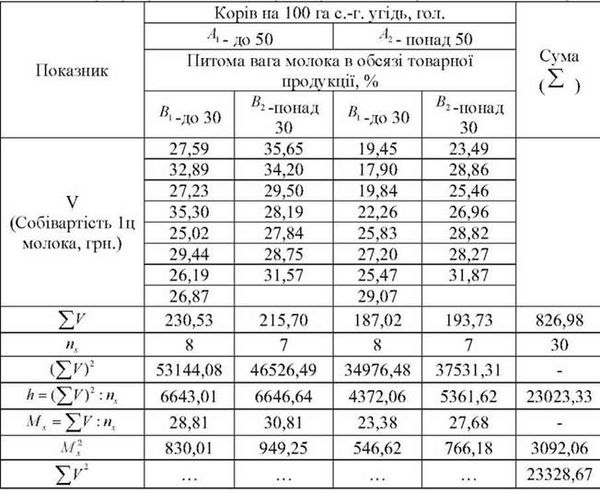
Ступінь впливу факторних ознак (концентрації її і спеціалізації виробництва) на результативну ознаку (собівартість виробництва молока)

Ті - ^ - ^ = 0,4262 С 53214

Становитиме : У (42,6 %). Ступінь впливу неврахованих

С_^__ 305,34 = 0,5738 С 53214

Факторів на результативну ознаку буде: У (57,4 %).

Для кількісної характеристики впливу кожного з факторів слід дисперсію

Їх сумарної дії розкласти на складові, тобто в факторній дисперсії ( * )

Виділити дисперсії першого ( а ) і другого ( ") факторів, а також їх сполучення

(^АВ).Дисперсія ^ав характеризує ступінь зумовленості впливу першого фактора другим. Складемо допоміжну таблицю 49. Третя колонка цієї таблиці розраховується на основі даних таблиці 49.

59,62=28,81 +30,81; 52,19 = 28,81 + 23,38

Таблиця 49

Допоміжні розрахунки для обробки дисперсійного комплексу за факторами А, В

Градація, і

Число середніх, і

' і

М2

2

59,69

29,81

888,63

2

51,06

25,53

651,78

110,68

£М2 = 1540,41

2

52,19

26,10

681,2100

ВГ

2

58,49

29,24

854,9776

110,68

£М2 = 1536,1876

Середня арифметична (загальна) по градаціях факторів становить: М = *Ь. = 11068 = 27,67.

Ступінь різноманітності середніх арифметичних собівартості 1ц молока розраховуємо в такій послідовності :

С' = ІЖ _ мі ] = 30[3^ - 27,672 } = 221,70; для всіх градацій - VА* ) ^ '

_ Й№і_Мі] = 30Г154!41-27,672] = 137,10 для градації ^ ~ =чЛ ^ ;

В _ С. = Л£І _ мі ] = 30Г1536,19 - 27,672 ] = 74,10 для градації ^ В ) ;

Для сполучення факторів

А і В ~ = С* ~ С'А ~С'В = 221,70 - 137,10 - 74,10 =10,50 Для розкладу сумарної дисперсії досліджуваних факторів на складові розраховуємо поправочний коефіцієнт:

К = ^ = 226,80 = 1,023. С'Х 221,70

Дисперсії, зумовлені дією досліджуваних факторів і їх сполучення, становлять С Л = С'аК = 137,10-1,023 = 140,25; СВ = С'В К = 74,10-1,023 = 75,81; САВ = С'АВК = 10,50 o 1,023 = 10,74.

Кінцева дисперсійна структура двофакторного дисперсійного комплексу

С = (С, + С" + С,") + С7 = 226,80 + 305,34 = 5320,14. матиме вигляд: У ■ А В АВ' Г

Розраховуємо ступінь впливу факторів, що вивчаються, на формування

Змінюваності результативної ознаки. Зокрема, рівень концентрації поголів'я

__ С1 = ИОД5 = 0,2636,

С 53214

Корів визначає варіацію собівартості 1 ц молока У або

Гі __ = ^ = 01425, С 53214

26,36 %; фактор спеціалізації - У або 14,25; взаємодія

, = = ^О1! = 0,0202, С 53214

Факторів - У або 2,02 %.

Числа ступенів вільності для розрахунку девіати в двофакторному

Комплексі розраховуються в такій послідовності : У Л = ІЛ ~1 = 2 ~1 = 1; уВ = їВ -1 = 2 -1 = 1; уАв = їЛ ■ їВ = 1; уХ =уА + уВ +уЛв = 3; уГ= П - ЇА ■ їВ = 30 - 4 = 26. Визначаємо девіати :

АА =£. = 140,25 = 140,25; *1 =^ = 1581 = 15,81;

<в = ^ = Ш^ю,^ Д1 = ;226!80 = 15,60;

УА В 1 у, 3

О* = = 305,34 = 11,14.

УГ 26 Розраховуємо Б - критерій: РЛ =£ = = 11 =£ = 75,81 = 6,45;

О 11,14 о 11,14

РЛ, = 1024 = 0,91; р = 4 =15,60 = 6,44.

ЛВ о 11,14 * ст2 11,14

Одержані критерії порівнюємо з табличними їх значеннями при двох порогах імовірності 0,95 і 0,99 (додатки 8,9).

Стандартні відношення девіат, які відповідають ступеням вільності

Варіації неврахованих факторів (Уг = 26) і розрахованим вище ступеням вільності варіації досліджуваних факторів становитимуть:

Імовірність Р Критерій Б

При "1 = 1 При "3 = 3

0,95 4,22 2,98

0,99 1,12 4,64

Результати аналізу кожного з факторів окремої чи сумарної їх дії слід вважати вірогідними при тих порогах імовірності, де

РР > РТ. Недостовірними при Рр < Р.

Приклад. Розглянемо послідовність розрахунку трифакторного дисперсійного комплексу на прикладі вивчення залежності собівартості виробництва 1ц яловичини (V) від рівня продуктивності праці (А) , рівня витрат кормів на 1 ц приросту (В) і собівартості 1ц кормових одиниць (С). З метою кількісної оцінки названих вище факторів на результативну ознаку будуємо трифакторний дисперсійний комплекс, основу якого становить комбінаційне групування 66 підприємств (табл. 50).

Досліджувану сукупність спочатку розподілено на дві групи: з рівнем

Затрат робочого часу на виробництво 1 ц яловичини до 90 людино - годин. понад 90 людино - годин (^2). У кожній групі було виділено по дві підгрупи з середнім розміром витрат кормів на 1 ц продукції: менше 10 (^) і більше 10 ц

Кормових одиниць. (^2). Потім кожна з них у свою чергу розподілена ще на дві підгрупи: з собівартістю 1 ц кормових одиниць, згодованих тваринам, до 14

С с

Грн.^1) і понад 14 грн. ( 2). У результаті досліджувана сукупність підприємств

Була розподілена на 8 підгруп, по кожній з яких наведено варіанти

Результативної ознаки (V) - рівень собівартості виробництва 0,1ц яловичини.

Оскільки у нашому прикладі розглядається трифакторний нерівномірний

Комплекс, обробку його здійснюємо в такій послідовності: спочатку будуємо

Звичайним чином кореляційну решітку, потім виконуємо допоміжні

Розрахунки, результати яких заносимо в цю ж таблицю. До них відносяться

УУ

Кількість ("=66) і сума (*-o ) варіант досліджуваного комплексу, сума часток від ділення квадратів сум варіант по кожній підгрупі на число варіант У Н

=669887,82), сума квадратів середніх арифметичних по підгрупах (У^м2 = 78826.00)

С

На підставі розрахункових даних таблиці 50 визначаємо загальну ( У),

С с

Факторну ( *) і залишкову ( ^ ) дисперсії:

С =УТ2 - ) = 672890,20 - 6599,772 = 12936,20;

(У V)2 6599 772 С =У НГ -^'= 669887,32--99-= 9933,32;

Є; = ^V2 - £Н1 = 672890.20 - 669887.32 = 3002.88

Встановлюємо частку всіх досліджуваних факторів у загальній варіації результативної ознаки. Так, ступінь впливу продуктивності праці, розміру

...... ,1 - І9333! = 0,768,

Витрат і вартості кормів на рівень собівартості становить : 12936,20

2 3002,88

ЛІ =-'- = 0,232,

Або 76,8%; а суми неврахованих факторів - 12936,20 АБ0 23,2%.

Як відзначалося вище, у багатофакторних комплексах дисперсія спільної

Дії врахованих факторів ( *) підлягає розподілу на дисперсії кожного з

Ссе

Факторів окремо ( А' В' С), а також дисперсії різних варіантів їх сполучень (С С С С )

^ аво Ав> ас> вс) . у нерівномірних комплексах всі часткові дисперсії факторів відрізнятимуться від величин таких же дисперсій в рівномірному комплексі, тому позначимо їх через С.

Допоміжні розрахунки для визначення окремих дисперсій показані у таблицях 51 і 52.

Таблиця 50

Обробка трифакторного дисперсійного комплексу

(А - групи підприємств за рівнем продуктивності праці, людино-годин на 1 ц ; В - розмір витрат кормів на виробництво 1ц яловичини, ц корм, од.; С - собівартість 1ц кормових одиниць, згодованих худобі, грн;

V - рівень собівартості 0,1ц яловичини, грн.; И' - кількість підприємств)

Групи та підгрупи за факторами

Вихідні і розрахункові дані

1А = 2; 4 = 2; /С = 2

V

Щ

ТУ

"і

2у

4

1 "до

90

А - до 10

СІ - до 14

76,76; 75,74...

4

278,01

77289,56

19322,39

19676,70

69,50

4830,25

Понад 14

87,74; 92,09...

9

866,53

750874,24

83430,47

83792,93

96,28

9269,84

В2_

Понад 10

СІ - до 14

84,44; 92,84...

8

733,03

537332,98

67166,62

67376,62

91,63

8396,06

С

2 понад 14

104,88; 102,08...

6

657,06

431727,84

71954,64

72144,87

109,51

11992,44

А.

Понад 90

Діло ю В2 _ Понад 10

СІ - до 14

85,84; 98,66...

10

902,86

815156,18

81515,62

81919,98

90,29

8152,28

С2_

Понад 14

107,17; 102,49...

9

966,59

934296,23

103810,69

104154,52

107,40

11513,29

С. _ до 14

10126; 103,22...

11

1117,69

1249230,94

113566,45

111971,19

101,61

10324,59

Понад 14

123,48; 118,42...

9

1078,00

12920,44

129120,44

129673,92

119,78

14347,25

Сума

6599,77

66

-

-

669887,32

672890,20

-

78826,00

Ступінь відмінності по всіх факторах визначаємо за вище наведеною формулою:

Таблиця 51

Допоміжні розрахунки для обробки дисперсійного комплексу за факторами А, В, С

О "

Розрахункові дані

Групи і підгрупи за факторами

Число середніх (

Число спостереже

(")

М, = ^ ' і

М2

ТУ

П

4

27

366,92

8414,39

2534,63

2534,63

93,87

4

39

419,08

104,77

10976,75

4065,14

104,23

Показники по фактору

66

786,00

-

19391,14

6599,77

100,00

А

В,

4

32

363,47

90,87

8257,36

301,99

91,19

4

34

422,53

105,63

11157,70

3585,78

105,46

Показники по фактору В

66

786,00

-

19415,06

6599,77

100,00

С,

4

33

353,03

88,26

7789,83

3031,59

91,87

СГ

4

38

432,97

108,24

11715,90

3568,18

108,18

Показники по фактору С

66

786,00

-

19505,73

6599,77

100,0

Таблиця 52

Допоміжні розрахунки для обробки сполучень факторів

Підгрупи за факторами

Число середніх (1)

Розрахункові дані

Ум, І

М2

4 А

2

165,18

82,89

6810,15

2

201,14

100,51

10114,32

2

191,69

98,84

9169,35

4 В2

2

221,39

110,69

12252,28

186,00

-

ЕМАв =39006,10

2

161,13

80,56

6489,91

А ^2

2

205,19

102,89

10586,35

2

191,90

95,95

9206,40

А2 С2

2

221,18

113,59

12902,69

186,00

-

2>'с =39185,35

В, С1

2

159,19

19,89

6382,41

2

203,68

101,84

10311,39

В2 С1

2

193,24

96,62

9335,42

В2 С2

2

229,29

114,64

13142,33

189,00

-

ЕМ'с =39231,55

За даними таблиць 51 і 52 визначаємо ступінь вільності середніх арифметичних для об'єднаних факторів : А і В - С™ = "(Аав ~ КК~ ^ + М"),

ІМ^ = 3900610 = 9151,01;

Де а 'в ^ ^

УМ2 19391 14 к, =^-^ = 19391,14 = 9695,51

М = Г941506 = 9101,53. І 2

Отже,

С'АВ = 66(9151,61 - 9695,51 - 9101,53 + 9653,06) = 101,58.

Аналогічно розраховуємо часткові дисперсії для інших сполучень факторів:

А і С - С'АС ~ 66(9196,34 - 9695,51 - 9152,86 + 9653,06) = 64,02;

В і С - СВ с = 66(9801,89 - 9101,53 - 9152,86 + 9653,06) = 36,96;

А, В, С

С'АВС = 13212,54 - 2805,66 - 3595,02 - 6586,80 -101,58 - 64,02 - 39,96 = 16,50.

С 9933 32

Знаходимо поправочний коефіцієнт К = - =-'■--0,1518.

Г С'Х 13212,54

Для виправлення часткових дисперсій С*, Сд, Св, Сс, Сдв, Сдс, Св С, Сдвс множимо на їх поправку 0,7512 і результати заносимо в другий рядок таблиці 54. Ступінь впливу досліджуваних факторів у формуванні загальної мінливості собівартості визначається відношенням часткових дисперсій по факторах (СА; СВ;;СС) І Їх Сполучень (Сав;САс;СВс;САВС) До Загальної дИСПерсії ^ У нашому прикладі для фактора А (затрати живої праці на 1ц приросту)

С, 12936,20 ,

У ' тобто в умовах досліджуваних підприємств варіація

Продуктивності праці становить 16,3 % варіації собівартості виробництва

Продукції.

Фактор В ( розмір витрат кормів на виробництво 1ц яловичини) становить 20,9 % коливання показника рівня собівартості, а фактор С (вартість 1ц корм. од.) - 38,3 %. Частка впливу у зміні рівня собівартості взаємодії факторів характеризується такими даними: А і В - 0,6 %; А і С - 0,4 %; В і С - 0,2 %; А, В і С - 0,1 %.

Знаходимо число ступенів вільності варіації, які в трифакторному

Дисперсійному комплексі обчислюють у такому порядку : У&; = 1 = 1; уВ = іВ-1 = 1; УС = ІС-1 = 1; уАв=уЛ-уВ = 1; vAC =vAOvC = 1; УВс = vВOvC = 1;

^двс = УЛ ■Ув-Ус = 1; V, = УА+^+^с +^ав +^ас +^вс +^авс = 7.

Сума часткових ступенів вільності повинна давати їх число для загальної

Дисперсії У ' 1

Девіати, розраховані за даними нашого прикладу, наведені у таблиці 53 по рядку 5.

Вірогідність дії факторів і їх сполучень визначаємо, як і раніше відношенням факторних девіат і їх сполучень до залишкової девіати. Для нашого прикладу наведені по рядку 5 таблиці величини девіат ділимо на залишкову дисперсію 51,77. Обчислені значення коефіцієнтів Р записуємо по рядку 6.

Зіставляючи обчисленні та табличні значення Р критеріїв бачимо, що

Загальнофакторна дисперсія * і дисперсії, викликані кожним з досліджуваних факторів, достовірні при всіх порогах імовірності (Р=0,95 ; Р=0,99 ; Р=0,999),

Оскільки Р > ГТ. Дисперсії, зумовлені сполученнями (при всіх можливих варіантах) факторів, виявились невірогідними.

Таблиця 53

Зведена інформація результатів лічильної обробки трифакторного дисперсійного комплексу

Статистичні характеристики

Умовні позначення

А

В

С

АВ

АС

ВС

АВС

X

Г

У

Дисперсія

Невиправлена

С

2805,66

3595,02

6586,80

107,58

64,02

36,96

16,90

13212,54

Виправлена

С = С'-К

2109,29

2702,74

4951,96

80,88

48,13

27,79

12,40

9933,32

3002,88

12936,20

Коефіцієнт співвідношення

0,163

0,209

0,383

0,006

0,004

0,002

0,001

0,768

0,232

1,000

Число ступенів вільності

V

1

1

1

1

1

1

1

7

58

65

Девіата

А1

2109,29

2702,74

4951,69

80,88

48,13

27,79

12,40

1419,04

51,77

-

Критерій Фішера

40,74

52,21

95,65

1,56

0,93

0,54

0,24

27,41

-

-

Розрахунковий

0,999

12,1

12,1

12,1

12,1

12,1

12,1

12,1

4,3

-

-

Табличний

Р Т 0,99 0,95

7,1 4,0

7,1 4,0

7,1 4,0

7,1 4,0

7,1 4,0

7,1 4,0

7,1 4,0

3,0 2,2

-

-

Схожі статті




Статистика - Опря А. Т. - 7.1.2. Алгоритми рішення дисперсійних моделей

Предыдущая | Следующая