Статистика - Опря А. Т. - 7.2.2. Рівняння регресії, визначення його параметрів

Рівняння, що відображує зміну середньої величини однієї ознаки (у) в залежності від другої (х), називається рівнянням регресії або рівнянням кореляційного зв'язку.

При простій кореляції це рівняння має вигляд:

У, =АО +аІХ

Де У* ~ середнє теоретичне значення У при даному значенні х; - параметри рівняння. Кореляційне рівняння пов'язує результативну ознаку з факторною у вигляді рівняння прямої лінії, де параметр "і визначає

Немчинов B. C. Избранные произведения. Т.-2 - М.: Наука, 1967.- С.439 середню зміну результативної ознаки (у) при зміні факторної ознаки (х) на одиницю її натурального виміру.

Невідомі параметри А° і "і знаходять за способом найменших квадратів, який ставить умову, щоб сума квадратів відхилень у від

Аплікат У*, обчислених за рівнянням регресії, була найменшою, або, інакше кажучі, щоб при зображенні в прямокутній системі координат теоретична лінія регресії проходила б максимально близько до фактичних даних. Такій умові відповідає пряма, параметри якої є коренями системи нормальних рівнянь:

К,"+"1У Х = ~е У

[А0 £ Х+А1 Л Х 2 =Л Ху.

Приклад. Розглянемо кореляційну залежність між затратами праці на виробництво одиниці продукції (у) і рівнем автоматизації процесів в 64 підприємствах.

За даними спостереження вирахуємо допоміжні величини (табл. 54). Підставивши в систему нормальних рівнянь замість буквених позначень обчислені сумарні значення, одержимо :

[64А0 + 40,96а1 = 156,38;

[40,96А0 + 21,521а1 = 98,9120

Таблиця 54

Вихідні і розрахункові дані для обчислення параметрів _Кореляційного рівняння_

Дані спостереження по 64 підприємствах

Розрахункові величини

Затрати праці на одиницю, люд.-днів

У

Показник рівня автоматизації

X

Ху

Х2

У2

1,39

0,82

1,2398

0,6124

1,9321

1,54

1,00

1,5400

1,0000

2,31116

Всього 156,38

40,96

98,9120

21,5216

419,9248

Порівняємо коефіцієнт при невідомому 00 і віднімемо з першого рівняння друге:

А0 + 0,6400А1 = 2,4434 - а0 + 0,6121А1 = 2,4163 - 0,0321а1 = 0,0211

Звідки

АХ = 0,02771 = -0,8442. 1 0,0321

Підставимо значення параметра

"1 = ~0,8442 у ПЄРШЄ рівняння, обчислимо значення параметра А": а0 + 0,6400(-0,8442) = 2,4434; А0 = 2,4434 + 0,5403; а0 = 2,9837

Таким чином, рівняння лінії регресії прийме такий аналітичний вигляд:

¥Х = 2,9837 - 0,8442х

Гт ■ ■ ■ У = 156 38: 64 = 2 44-

Перевірка правильності рішення: ±->и, л>.^

Х = 40,96 : 64 = 0,64; ~у = 2,98 - 0,84 o х = 2,98 - 0,84 o 0,64 = 2,98 - 0,54 = 2,44.

Для зручності інтерпретації виразимо х (факторну ознаку) в відсотках. У

Цьому випадку коефіцієнт при х зменшиться в 100 разів.

Таким чином, у загальному вигляді рівняння матиме вигляд:

У, = 2,98 - 0,008х

Економічна інтерпретація даного кореляційного рівняння така: збільшення рівня автоматизації процесу на 1% призводить до зменшення витрат живої праці на одиницю продукції в середньому на 0,008 людино - дня.

7.2.3. Криволінійна регресія

При криволінійній формі зв'язку збільшення факторної ознаки призводить до нерівномірного збільшення (або зменшення) результативної ознаки, або ж зростання її величини змінюється спаданням, а зменшення - збільшенням.

Для визначення зв'язку між ознаками, взаємовідношення яких передбачає можливість існування оптимальних розмірів операцій, використовують рівняння параболи:

УХ = а0 + а1Х + аГ х1.

Одна з особливостей цього типу кривої та, що вона завжди має точку перетину (критичну точку), яка характеризує оптимальний варіант розміру величини результативної ознаки, і змінює напрямок свого руху лише один раз. Якщо в рівнянні величина А1 виражена від'ємним числом, а А2- додатним, то крива змінюватиме напрямок спаду на зростання.

Для розрахунку параметрів рівняння параболи другого порядку використовується така система нормальних рівнянь:

А0П + х + аГ ^ х1 = Ну:

" А0 2 Х + АТ" х1 + АГ 2 ХІ = ^ХУ; а0 ^ х1 х3 +а2 ^ х4 = Бх2 У.

Приклад. Розглянемо залежність собівартості одиниці продукції від рівня спеціалізації виробництва (х, %) на прикладі 20 підприємств. Для рішення рівняння параболи підставляємо в систему нормальних рівнянь відповідні, попередньо розраховані, підсумкові дані. Отже, одержимо

Г20а0 + 1111,58а! + 15489,18а2 = 2033,04;

І1111,58а0 + 15489,18а1 + 5180169,86а2 = 121585,39;

[15489,18а0 + 5180169,86а1 + 311409983,95а2 = 8001658,22.

Розв'язавши цю систему рівнянь, знаходимо значення параметрів: а0 = 132,95; аХ = -1,19; а2 = 0,02.

Рівняння зв'язку у даному випадку має такий аналітичний вигляд : У, = 132,95 -1,19* + 0,02л:2.

Застосування гіперболічної форми кореляційного зв'язку розглянемо на прикладі залежності рівня виробничих витрат на одиницю продукції (у) від об'єму її виробництва (х).

Відомо, що загальна сума затрат виробництва ділиться на дві групи. До першої відноситься сума витрат, яка залежить від кількості виробленої продукції. Ця група включає вартість використаної сировини і затрати на оплату праці. Друга група витрат містить в собі суму витрати, які не залежить або непрямо залежних від об'єму виробленої продукції. До них відносять амортизацію, поточний ремонт, інші основні і накладні витрати. Позначимо

7

Суму витрат першої групи, яка припадає на одиницю продукції, через °' кількість виробленої продукції - через х. Загальна сума витрат цієї групи

Становить ^°*. Суму витрат другої групи позначимо через Тоді загальна

Сума витрат буде Ху ~ Х + Щоб визначити рівень витрат, які припадають на одиницю продукції, потрібно отриманий вираз поділити на х. Ця залежність

Матиме вигляд: Х

Даний вираз нагадує рівняння гіперболи:

X

Таким чином, залежність рівня витрат виробництва продукції від виробленої її кількості може бути виражена рівнянням двочленної гіперболи. Параметри цього кореляційного рівняння визначаємо за такою системою рівнянь:

А0И + а1Е - = ЕУ; х

1 1 2 1

А1І - + а1І(-)2 =1 - У.

Використовуючи попередньо розраховані підсумкові дані по 66 підприємствах, запишемо наведену систему рівнянь у вигляді:

[66а0 + 111,8938а1 = 840,9200; ]111,8938а0 + 260,1022а1 = 1419,1429.

Розв'язавши ці рівняння, одержимо наступні числові значення параметрів: "0 = 12,8826; "! = 0,0834.

Шукане кореляційне рівняння зв'язку собівартості одиниці продукції та об'єму її виробництва матиме вигляд:

У, = 12,88 + -0,08.

Х

Якщо інтервал зміни факторної ознаки значний, використовують рівняння тричленної гіперболи:

Ух = а0 + а1Х + а2 - х.

Система нормальних рівнянь у даному випадку буде наступною:

А0П + а^Ех + а2£ - = Ху;

Х

- а01,х + а1£х2 + а2П = Іху; .

1 1 2 1

А0£-Іа1П + а2£(-) = £-У

У прикладі, який розглядається, ця система має вигляд: Г66А0 + 51,2349а! + 111,8938а2 = 840,9200; | 51,2349а0 + 52,5861а! + 66а2 = 611,0019; [ш,8938а0 + 66а1 + 260,1022а2 = 1419,1429

Розв'язавши наведену систему рівнянь, одержимо числове значення параметрів: А° = 12,6401; "1 =0,8694; "2 =0,3388. Відповідно, кореляційне рівняння зв'язку матиме вигляд:

- 034

Ух = 12,64 + 0,81 х + ^- х.

Для аналітичного виразу явищ, які відносяться до вивчення темпів росту, використовують рівняння експонентної кривої:

У,. =А° ■ "1, дЄ а - фактор - аргумент (порядковий номер року, який в аналітичних рівняннях динаміки одержує значення 1,2, 3 і т. д.), "0-показник базисного року; А1 ~ середньорічний темп зростання.

Невідомі параметри "0 і А1 у наведеній вище формулі визначають логарифмуванням, перетворивши показникову функцію в пряму: І8У = 1%А0 + Х1^А1.

Система нормальних рівнянь при цьому має вигляд:

Гп + lgaLIx = ^ у; [lga0Lx + ^а^х1 = lg уІ, х

Приклад. Розглянемо зміну затрат праці на одиницю продукції (у) у підприємствах адміністративного району за десятирічний період

(1994-2003 рр.) Як відомо, показник затрат праці на одиницю продукції має завжди позитивне значення. При зниженні його рівня крива асимптотично (поступово) наближається до осі абсцис, але ніколи не може стати прямою, перетворитися в нуль або перетнути горизонтальну вісь (рис. 23), Оскільки суспільство не може виробляти продукцію без затрат праці. У Цьому випадку показники динаміки змінюються в геометричній прогресії.

Підставляючи попередньо розраховані сумарні показники для нашого прикладу в наведену вище систему нормальних рівнянь; одержимо:

Ш%а0 + = 3.77;

[55^а!0 + 385^ = 20.44.

Розв'язавши цю систему рівнянь, одержимо логарифми числових значень

Невідомих параметрів : ^ = 0.39592; ^ = 0.00347.

Визначивши антилогарифми, знайдемо значення параметрів: а0 = 2,49; = 0,99.

Одержане рівняння зв'язку матиме аналітичний вигляд: У' = 2,49'0,99 . Дане рівняння має таку економічну інтерпретацію: середні затрати праці на одиницю продукції в підприємствах району в нульовому періоді (1993 р.) досліджуваного відрізку часу складають 2,49 Люд.-дня, а зниження їх в кожному наступному періоді становить 1 %.

В аналізі економічного явища часто використовують степеневу функцію виду У = СС0 Х Нелінійність відносно своїх констант зумовлюють її перетворення (шляхом логарифмування) в логарифмічно - лінійну функцію виду 1еУ = "0 Х.

Таке перетворення дає можливість розв'язувати систему нормальних рівнянь методом найменших квадратів.

Застосовують логарифмічну лінійну функцію для явищ, характерних тим, що в міру приросту абсолютної величини факторної ознаки її вплив на результативну ознаку знижується. Для цього типу функції характерна пропорційність не абсолютних приростів (як для рівняння прямої лінії), а відносних приростів економічних показників, які вивчаються.

Якщо природа взаємовідношень економічних явищ така, що середня арифметична результативної ознака (у) пов'язана із середньою геометричною факторні ознаки (х), то математичний вираз подібної залежності, тобто оцінку однієї змінної по другій, дає логарифмічна крива, гіпотетичне рівняння якої : У = СС0 Х

Відсутність числових значень логарифмів для нульових і від'ємних чисел обмежує можливості у використанні логарифміческих функцій в окремих випадках економічного аналізу.

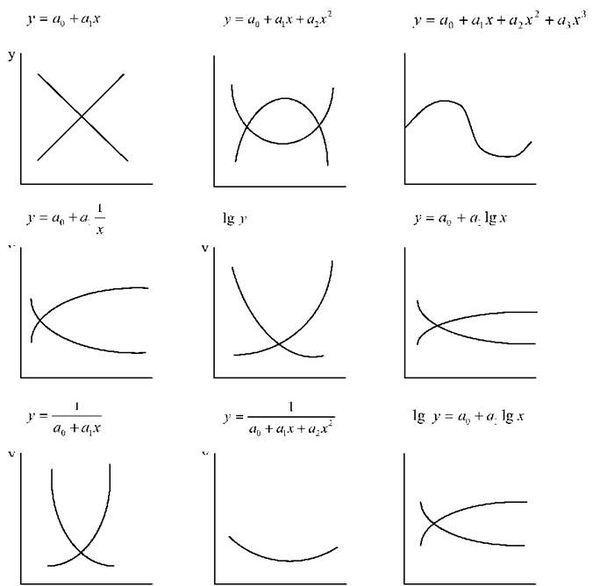
Рис 21. Лінії основних математичних функцій

На рисунку 21 представлені графічні зображення ліній основних математичних функцій.

Наявність випадкових факторів зумовлює ймовірнісний характер висновків про ступінь тісноти зв'язку. При цьому значення коефіцієнта кореляції, як і інших кореляційних характеристик, оцінюють на вірогідність. Суть такої оцінки міститься в зіставленні систематичної варіації результативної ознаки, зумовленої варіацією факторної ознаки, з випадкової варіацією (помилкою) результативної ознаки. З цією метою використовують критерії Ст'юдента і критерії Фішера.

И

Критерій Ст'юдента розраховується за формулою Мц

Де - середня помилка вибірки коефіцієнта кореляції, яка

1 - И2

Обчислюється за відношенням: ~1.

Одержане значення ір зіставляють з його табличним значенням (додаток 1) і роблять висновки про вірогідність коефіцієнта кореляції. Його величина визнається вірогідною, якщо іР>

У практичних розрахунках, для оцінки надійності коефіцієнта кореляції як правило, використовують таблиці вірогідних значень коефіцієнтів кореляції для відповідної кількості спостережень, тобто даного об'єму і рівня ймовірності (додаток 11).

Оскільки сам коефіцієнт кореляції є свого роду критерієм надійності досліджуваної залежності факторних і результативних ознак то висновок про його вірогідність може бути поширений на інші параметри кореляційно - регресійної моделі в цілому.

Схожі статті




Статистика - Опря А. Т. - 7.2.2. Рівняння регресії, визначення його параметрів

Предыдущая | Следующая