Теорія статистики - Мармоза А. Т. - 3.9. Показники диференціації ознак у сукупності

Для вивчення ступеня нерівномірності розподілу певного показника між одиницями окремих груп варіаційного ряду розподілу в статистиці можуть бути використані різні показники диференціації. До таких показників належать коефіцієнт і крива Лоренца і коефіцієнт (індекс) Джині.

Ці показники диференціації одержують шляхом зіставлення двох простих структурних рядів розподілу, один з яких виражає розподіл одиниць сукупності (наприклад, населення), а другий - обсяг належної цим одиницям ознаки (наприклад, грошового доходу).

Ступінь диференціації ознак у сукупності може бути визначена кількома способами: шляхом розрахунку показників диференціації, графічним методом, методом визначення коефіцієнта концентрації Лоренца, який також називають індексом Джині. Для всебічного вивчення ступеня диференціації доцільно використовувати всі три прийоми аналізу.

Розрахунок показників диференціації розглянемо на прикладі порівняння двох структурних рядів розподілу ("вертикальне сто") населення одного з регіонів країни за середньодушовим доходом. Для цього використаємо дані квінтільного (20%) розподілу населення за його чисельністю і доходом (табл. 3.12).

1. Розрахунок показників диференціації ведеться шляхом зіставлення по кожній групі питомої ваги (частини) числа одиниць і обсягу ознаки (гр. 3 табл. 3.12). Так, у першій групі з найменшими доходами на 20% населення припадає 6,0% грошових доходів. Показник диференціації одержують діленням питомої ваги ознаки (доходу) на питому вагу числа одиниць (населення; гр. 2: гр. 1, табл. 3.12). по групі 1 він становить 0,30 (0,06:0,20), по групі 2 - 0,55 (0,11:20), а по групі 5 - 2,20 (0,44:20).

Таблиця 3.12. Дані для розрахунку показників диференціації і коефіцієнта Джині

дані для розрахунку показників диференціації і коефіцієнта джині

При рівномірному розподілі на 1% населення припадає 1% грошових доходів. Як видно з даних таблиці, доходи по групах значно диференційовані. В групі 1 на 1% населення припадає всього 0,30% доходів, що нижче, чим у середньому в 3,3 разу (1:0,30), а в групі 5 - 2,20%. Різниця між 5-ю і 1-ю групами сягає 7,3 разу (2,20:0,30), що вказує на високу ступінь диференціації доходів населення.

2. Графічно ступінь диференціації відображають за допомогою побудови кривої американського статистика й економіста О. Лоренца (1876 - 1959). Для цього спочатку знаходять нагромаджені по групах підсумки часток населення і доходів, які наведені в розрахункових даних табл. 3.12 (гр. 4 і гр. 5). Потім на осі абсцис звичайно квадратного за формою графіка (100 х 100) відкладають відповідно до прийнятого масштабу нагромаджений відсоток чисельності населення (від найбідніших верств населення до найбагатших), а на осі ординат - відповідні їм нагромаджені відсотки доходів (рис. 3.7).

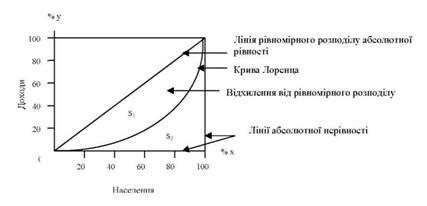
крива лоренца

Рис. 3.7. Крива Лоренца (побудова за даними гр. 4 і гр. 5 табл. 3.12)

Для кожної пари значень кумулятивних підсумків знаходимо точку перетину на графіку, проводячи перпендикуляри до осей координат. Одержані на графіку точки з'єднують кривою, яка називається Кривою Лоренца.

Чим більше відхилення кривої від діагоналі (бісектриси), тим більша нерівність у розподілі доходів, відповідно вища їх концентрація у високодоходних груп населення. При рівномірному розподілі на 1% населення припадає 1% доходів, на 10% населення - 10% доходів і т. д. Природньо, що чим більше фактичний розподіл відхиляється від рівномірного, тим більше крива Лоренца віддалена від діагоналі. Отже, чим більша ця віддаленість (угнутість), тим вища концентрація досліджуваного явища (в нашому прикладі доходів).

Якщо значення ознаки в групах варіаційного ряду розподілу дані у порядку зменшення (від більшого до меншого), то побудова за такими даними крива Лоренца буде розташована вище діагоналі у формі опуклості.

Декілька кривих Лоренца, побудованих на одному графіку, дають змогу порівнювати рівень концентрації досліджуваного показника в різний час по різних об'єктах.

3. Для кількісного вимірювання ступеня концентрації використовується коефіцієнт італійського статистика й економіста К. Джині (1884 - 1965), який також називається індексом Джині. Якщо у всіх громадян доходи однакові, то значення даного коефіцієнта дорівнює нулю. При припущенні, що весь доход концентрується в руках однієї особи (сім'ї, групи людей), значення коефіцієнта буде дорівнювати одиниці. Отже, фактичне значення коефіцієнта Джині знаходиться в інтервалі між нулем і одиницею. Із збільшенням значення цього коефіцієнта підсилюється нерівність.

Формула для розрахунку коефіцієнта Джині має такий вигляд:

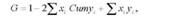
Де хг - частка населення, що належить і-й групі в загальній чисельності населення;

УІ - частка доходів, зосереджених в І - й групі населення.

Для нашого прикладу за даними таблиці 3.12 коефіцієнт Джині дорівнює:

Розрахований коефіцієнт свідчить про помірну диференціацію доходів населення.

Якщо користуватися в розрахунках не кумулятивними частками, а процентами, то результат обчислення слід поділити на 10000.

За кривою Лоренца можна обчислити коефіцієнт Джині як відношення площі між лініями рівномірного і фактичного розподілу до суми площ 51 і 52, яка

Дорівнює 1^:

Використання показників диференціації, розрахованих по групах населення, сформованих залежно від рівня доходів, збагачує можливості економічного аналізу і дає змогу кількісного виміряти ступінь нерівномірності розташування всередині окремих соціальних груп.

Схожі статті




Теорія статистики - Мармоза А. Т. - 3.9. Показники диференціації ознак у сукупності

Предыдущая | Следующая