Математична статистика - Руденко В. М. - Критерій Фрідмана X2 r

Критерій Фрідмана Хг застосовується для зіставлення показників, виміряних у трьох або більше умовах на одній і тій же вибірці і будується на рангових послідовностях. Критерій х2Г дозволяє встановити факт того, що значення показників від умови до умови змінюються, проте не указує на напрям цих змін.

Гіпотези:

Н0: між показниками, виміряними в різних умовах, існують лише випадкові розходження;

Н1: між показниками, виміряними в різних умовах, існують Невипадкові розходження.

Обмеження критерію: мінімальна кількість випробовуваних осіб п>2, кожна особа має пройти більше трьох випробувань с>3.

Приклад 5.19. На рис. 5.44 наведено результати самооцінки емпатичних здібностей студентів інституту (за методикою О. П. Єлісєєва). Чи достовірні розходження у значеннях самооцінки студентів у різні роки навчання?

Послідовність рішення:

O Формулювання гіпотез:

Н0: між показниками самооцінки емпатичних здібностей, виміряними в різні роки, існують лише випадкові розходження;

Н1: між показниками самооцінки емпатичних здібностей, виміряними в різні роки, існують невипадкові розходження.

O Перевірка обмежень: виміри зроблено за шкалою інтервалів; кількість умов С = 4 (с>3); кількість випробовуваних п =10 (п>2); вибірки зв'язані.

O Розрахунки емпіричного критерію ФрідманаX2Г (рис. 5.44):

- визначити середнє самооцінки за кожною умовою (для кожного курсу навчання), для чого у комірку В13 внести вираз =СРЗНАЧ(Б3:Б12). Аналогічні вирази внести у комірки С13:Е13;

- проранжувати індивідуальні значення самооцінки для кожного студента (ранжирування за рядками), нараховуючи меншому значенню менший ранг. Для цього у комірку В16 внести вираз

=(СЧЕТ($Б3:$Е3) + 1 - РАНГ(Б3;$Б3:$Е3; 1) -- РАНГ(Б3;$Б3:$Е3; 0))І2+РАНГ(Б3;$Б3:$Е3;1);

- аналогічні вирази внести у комірки всього діапазону В16Е25;

- у комірках В26Е26 підрахувати суми рангів Т за кожною умовою;

- у комірках Р16:Р26 перевірити збіг отриманих сум за рядками і за стовпчиками (суми рангів індивідуальних значень дорівнюватиме 10);

- у комірки В27:В28 внести значення параметрів п і с за допомогою функцій =СЧЕТ(Л3:Л12) і =СЧЕТ(В3:Е3);

- у комірці В29 підрахувати суму квадратів рангів за допомогою виразу =СУММКВ(В26:Е26);

- у комірку В30 внести вираз =12/В27/В28/(В28+1)*В29-3*В27*(В28+1), який дозволить підрахувати значення критерію Хг за формулою:

ХІ = - o£ (Т2) - 3 o п o (с +1), (5.28)

П ■ с ■ (с +1) 7=1

Де С - кількість умов; п - кількість випробовуваних осіб.

Як бачимо, значення емпіричного критерію Фрідмана У2Г ~ 15,39.

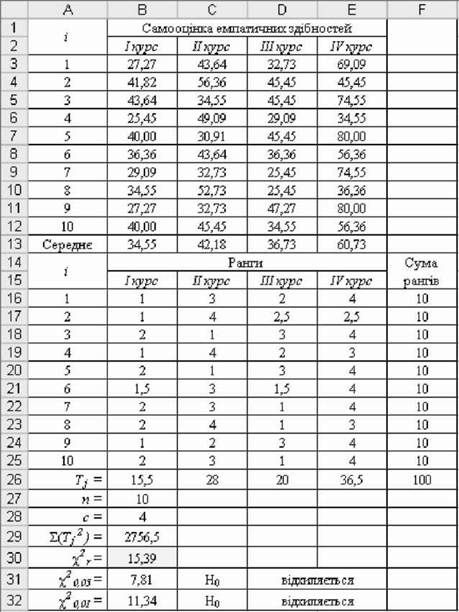
Рис. 5.44. Результати розрахунку критерію Фрідмана Хг

O Визначити критичні значення /2Г-критерію Для а=0,05 і 0,01 можна трьома способами, залежно від параметрів с і n:

- для С = 3 і N < 9 - з табл. 7 Додатків;

- для С = 4 і N < 4 - з табл. 8 Додатків;

- для с>4 або n>9 - за критичними значеннями /^-критерію.

Для а=0,05 і 0,01 і ступенів вільності v = c-l = 4-1= 3 критичні значення Х2О,05 ~ 7,81 і х2О, оі ~ 11,34 отримаємо за допомогою функції Excel =ХИ20БР(), яку необхідно внести у комірки В31 і В32 з відповідними аргументами: =ХИ20БР(0,05;3) і =ХИ20БР(0,01;3).

Прийняття рішення. Оскільки Хг > Хот (15,39>11,34), нульова гіпотеза Н0 відхиляється на рівні значущості 0,05 і 0,01 (див. рис. 5.44).

O Формулювання висновків. Між показниками самооцінки емпатичних здібностей, виміряними в різні роки навчання студентів, існують Невипадкові розходження на рівні значущості 0,01. Проте визначити тенденцію розходжень на підставі критерію Фрідмана неможливо, це дозволяє зробити критерій тенденцій Пейджа L.

Схожі статті




Математична статистика - Руденко В. М. - Критерій Фрідмана X2 r

Предыдущая | Следующая