Математична статистика - Руденко В. М. - Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Кохрана q для вибірок однакових обсягів)

Для перевірки гіпотези щодо дисперсій двох сукупностей, які представлені залежними вибірками використовується критерій Стьюдента і, статистика якого має вигляд:

Де S1 і 82 - дисперсії вибірок; п - кількість пар спостережень; Г 12 - квадрат коефіцієнта парної кореляції.

Методика перевірки гіпотези аналогічна попередньому прикладу.

Приклад 5.15. Виконати перевірку статистичних гіпотез щодо дисперсій П пар спостережень (емпіричні дані у таблиці рис 5.37).

Послідовність рішення:

O Формулювання гіпотез. Умовам перевірки однаковості дисперсії П пар спостережень відповідає варіант неспрямованих гіпотез:

Н0: а21 = а22 (а21 не відрізняється від а22); Н1: а21 Ф а22 (а21 відрізняється від А22).

O Перевірка припущень: досліджуваний параметр має Нормальний розподіл; вибірки Зв'язані; виміри проведено за шкалою відношень.

O Вибір статистичного критерію. Згідно з припущеннями цій ситуації відповідає модель двобічного і-критерію Стьюдента:

O Розрахунки емпіричного критерію і відповідні формули показано на рис. 5.37 і 5.38. Дисперсії вибірок s12 ~ 1,60 і s22 ~ 0,78, а також значення квадрату коефіцієнта кореляції Пірсона r212 ~ 0,17 розраховано за допомогою функцій MS Excel =ДИСП() і =КВПИРСОН(). Емпіричний критерій приймає таке значення:

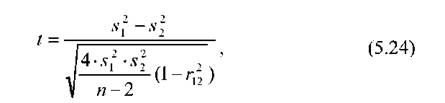
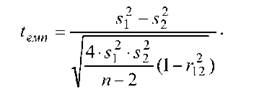
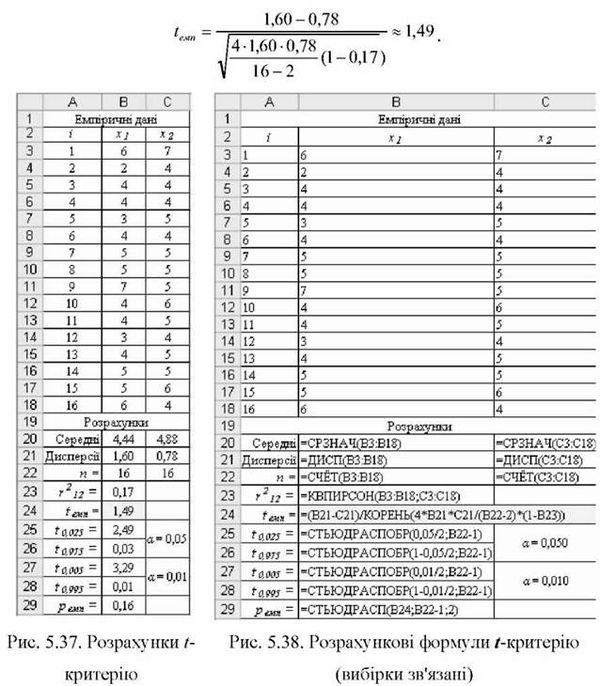
O Визначення критичного значення критерію. Для двобічної моделі встановлюються два критичні значення ГКр для точок (а/2) і (1-а/2) і-розподілу з числом ступенів вільності А/=п-2= 16-2=14, тобто: і А/2 і і 1-а/2. За допомогою функції =СТЬЮДРАСПОБР() для а = 0,05 отримаємо і 0025 ~ 2,49 і і ^975 ~ 0,03; для а = 0,01 і 0,005 ~ 3,29 і і 0,995 ~ 0,01 відповідно (рис. 5.37).

O Прийняття рішення. Оскільки значення і Емп~ 1,49 не знаходиться у жодній критичній зоні (0,03 < 1,49 < 2,49), приймається нульова гіпотеза Н0.

O Формулювання висновків. Навіть на рівні значущості 0,05 немає підстав стверджувати, що показники дисперсій відрізняються одне від одного.

Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Кохрана q для вибірок однакових обсягів)

Для перевірки гіпотез про рівність дисперсій 3-х і більш сукупностей використовується критерій Кохрана q.

Приклад 5.16. Виконати перевірку статистичних гіпотез істотності різниць дисперсій трьох незв'язаних вибірок за емпіричними даними рис. 5.39.

Послідовність рішення:

O Формулювання гіпотез:

H0: а21 = а22 = а23 (дисперсії між собою не відрізняються); H1: а21 Ф а22 Ф а2} (дисперсії між собою відрізняються).

O Перевірка припущень: досліджуваний параметр має Нормальний розподіл; кількість вибірок більша двох; вибірки Незв'язані однакових обсягів; виміри проведено за шкалою Інтервалів.

O Вибір критерію. Ситуації відповідає статистика критерію Кохрана q:

S 2

Max __.

Q = 2 ? , (5.25)

Де S21, s22, s2M - дисперсії вибірок; s2Max - максимальна дисперсія; M - кількість вибірок.

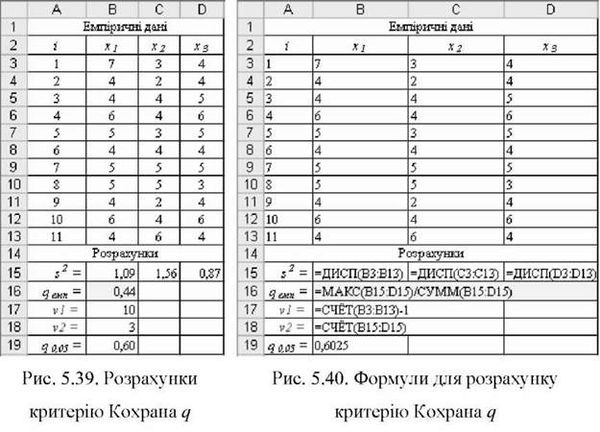
O Результати оцінки емпіричного критерію qEMn і додаткових параметрів показано на рис. 5.39. Значення дисперсій вибірок s2 розраховано за допомогою функції =ДИСП(), для отримання емпіричного критерію qEM" у комірку В16 введено вираз =MAKC(B15:D15)/CyMM(B15:D15), що відповідає елементарним розрахункам цього критерію:

1,56

Q =---яв 0 44

1,09 +1,56 + 0,87 ' '

O Критичне значення q-критерію Кохрана можна отримати за допомогою табл. 5 Додатків. На рівні значущості а = 0,05 для кількості ступенів вільності у1 = п-1 = 11-1=10 і у2 = Т = 3 критичне значення д0 05 ~ 0,60.

O Прийняття рішення. Оскільки дЕм"< д0і05 (0,44 < 0,60) приймається нульова гіпотеза Н0.

O Формулювання висновків. На рівні значущості 0,05 немає підстав стверджувати про те, що показники дисперсій відрізняються одне від одного.

Одна з переваг методу перевірки статистичних гіпотез за критерієм Кох-рана Д є простота обчислень. Недоліком вважається те, що критерій виявляє ознаки відхилення тільки у бік зростання.

Схожі статті




Математична статистика - Руденко В. М. - Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Кохрана q для вибірок однакових обсягів)

Предыдущая | Следующая