Математична статистика - Руденко В. М. - Критерій Колмогорова-Смірнова λ

Критерій Крамера-Велча Т побудований на підході оцінювання рівності математичних очікувань генеральних сукупностей, звідки взято вибірки. Статистика критерію має вигляд:

-у/П1П2 (х 1 " Х2)

= І 2 2 , (5.11)

^ 1 + П2 5 2

Де невідомі дисперсії замінені їхніми вибірковими оцінками. Більш того, при рості обсягів вибірок розподіл статистики Т Крамера-Велча збігається до стандартного нормального розподілу з математичним очікуванням 0 і дисперсією 1,00. З асимптотической нормальності статистики Т правило ухвалення рішення для критерію Крамера-Велча виглядає так: якщо ТЕм"< г(1-а/2), то гіпотеза однорідності (рівності математичних очікувань) приймається на рівні значущості а. У прикладній статистиці найбільше часто застосовується рівень значущості 0,05. Тоді значення модуля статистики Т Крамера-Велча треба порівнювати із критичним значенням гКр=1,96.

Приклад 5.6. Зробити статистичні висновки на рівні значущості 0,05 щодо однорідності двох вибірок за критерієм Крамера-Велча (емпіричні дані взято з попереднього прикладу 5.5).

Послідовність рішення:

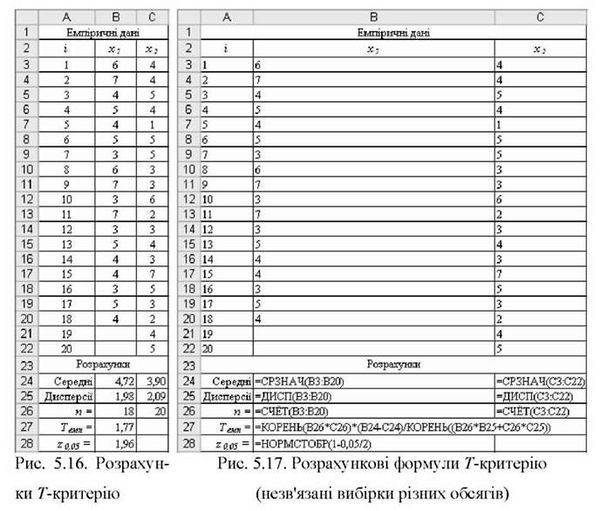
O Розрахунки емпіричного критерію показано на рис. 5.16 і 5.17. Емпіричне значення критерію ТЕм" можна оцінити з елементарних розрахунків:

Т _ V18 o 20(4,72 - 3,90) ^ 1 77 718 -1,98 + 20 o 2,09 ~ ' .

O Критичне значення ТКр для рівня значущості 0,05 отримаємо за допомогою функції =НОРМСТОБР(1-0,05/2), яка повертає значення 1,96.

O Прийняття рішення. Оскільки ТЕмп< г0о05 (1,77<1,96), нульова гіпотеза Н0 приймається на рівні значущості 0,05.

O Формулювання висновків. На рівні значущості 0,05 відсутні підстави стверджувати про неоднорідність незалежних вибірок.

Серед психолого-педагогічних завдань нерідко інтерес становить не перевірка рівності математичних очікувань або інших параметрів розподілу, а виявлення будь-яких розходжень генеральних сукупностей, з яких витягнуті вибірки. Але методи, що засновані на використанні статистик Стьюдента І і Крамера-Велча Т, не дозволяють перевіряти гіпотезу Н0 щодо розходжень сукупностей. Тому варто використовувати непараметричні методи (наприклад, Колмогорова-Смірнова, Вілкоксона-Манна-Вітні, Лемана-Розенблатта та ін.), для яких не є обов'язковими припущення приналежності розподілу результатів спостережень певному параметричному сімейству.

Критерій Колмогорова-Смірнова λ

Критерій Колмогорова-Смірнова x призначений для зіставлення двох емпіричних розподілів F1(x) i F2(x) між собою. Статистика критерію має вид:

А = max| F1 (x) - F2( x), (5.12)

Де F1(x) i F2(x) - емпіричні функції розподілу вибірок и1 і и2.

Критерій дозволяє знайти точку, у якій сума накопичених розбіжностей між двома розподілами F1(x) i F2(x) є найбільшою (максимальною), і оцінити достовірність цієї розбіжності. Для ^-критерію зіставляють Накопичені (інтегральні) частоти. Нульова гіпотеза H0 свідчить про те, що відмінності між двома розподілами Недостовірні.

Приклад 5.7. Зробити статистичні висновки на рівні значущості 0,05 щодо однорідності двох вибірок за критерієм Колмогорова-Смірнова (емпіричні дані взято з прикладу 5.5).

Послідовність рішення:

O Формулювання гіпотез:

H0: відмінності між двома розподілами Недостовірні (судячи з точки максимальної накопиченої розбіжності між ними);

H]: відмінності між двома розподілами достовірні (судячи з точки максимальної накопиченої розбіжності між ними).

O Розрахунки емпіричного критерію Колмогорова-Смірнова x Емп показано на рис. 5.18. У стовпчику J розраховано абсолютні різниці накопичених емпіричних частот | F1 - F2 |, максимальне значення яких складе емпіричний ^-критерій Колмогорова-Смірнова:

^емп = max| F1 - F2 | = 0,178. Розрахункові формули для визначення xЕмп наведено на рис. 5.19.

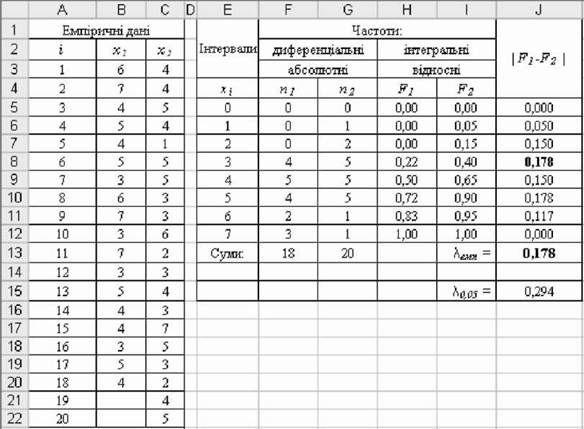
Рис. 5.18. Розрахунки емпіричного критерію X

O Критичні значення ^-критерію для рівня значущості 0,05 і П = 20 визна-

Чаються за табл. 3 Додатків!0_05~ 0,294.

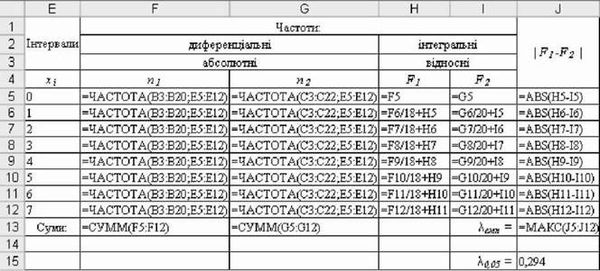
Рис. 5.19. Розрахункові формули для визначення XЕмп

O Прийняття рішення. Оскільки емпіричне значення критерію ^Е^"~0,178 менше за критичне значенню Х0 05 ~ 0,294, гіпотеза Н0 приймається на рівні значущості 0,05.

O Формулювання висновків. На рівні значущості 0,05 відсутні підстави стверджувати про неоднорідність незалежних вибірок.

Схожі статті




Математична статистика - Руденко В. М. - Критерій Колмогорова-Смірнова λ

Предыдущая | Следующая