Математична статистика - Руденко В. М. - Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Бартлета М для вибірок різних обсягів)

Критерій Бартлета вважається найпотужнішим для перевірки гіпотези щодо рівності дисперсій для ознак з нормальним розподілом. Він не є обмеженим попарними порівняннями і дозволяє одночасно порівнювати декілька дисперсій.

Приклад 5.17. Виконати перевірку статистичних гіпотез щодо істотності різниць дисперсій п'ятьох незв'язаних вибірок за емпіричними даними рис.

5.41.

Послідовність рішення:

O Формулювання гіпотез для варіанта неспрямованих гіпотез:

2 2 2 2 2

Н0: а 1 = а 2 = а 3 = а 4 = а 5 (дисперсії між собою не відрізняються);

2 2 2 2 2

Н1: а 1Ф а 2 Ф а 3 Ф а 4 Ф а 5 (дисперсії між собою відрізняються).

O Перевірка припущень: досліджуваний параметр має Нормальний розподіл; чисельність вибірок більша двох; вибірки незв'язані різних обсягів; виміри зроблено за шкалою Інтервалів.

O Вибір статистичного критерію. Ситуації відповідає статистика двобічного критерію Бартлета м.

М = -, (5.26)

±у± емп ^ ' v '

Т т

Де М = 2,3026 o (^(у 2) o £ п} (пу o ])); т - кількість вибірок; ц і я 7 - обсяги і дисперсії вибірок (/ = 1, 2, т);

O Послідовність розрахунку критерію Бартлета (рис. 5.41 і 5.42):

- у комірках Н3:Ь3 і Н4:Ь4 розрахувати обсяги п і дисперсії вибірок я/;

- у комірках Н5:Ь5 розрахувати десяткові логарифми дисперсій вибірок ^(.у 2 ) за допомогою функції =ЬОв10();

- у комірці Н6 знайти середнє арифметичне порівнюваних у2, яке можна

Оцінити елементарними розрахунками:

2 0,84-15 + 0,92-13 +1,05-16 +1,76-14 + 0,57 o 8 , ""

Я 2 = ----------"1,07;

15 +13 +16 +14 + 8

У комірці Н8 розрахувати значення:

2) o Е П} = ^(1,0702) o (15 +13 +16 +14 + 8) * 1,95;

У комірці Н9 розрахувати значення:

]Г(п,. o 1@(у2)) = 15- (-0,08)+13- (-0,03) + 16- 0,02+14- 0,25+ 8 o (-24) * 0,24;

7=1

У комірках Н10, Н11 і Н12 розрахувати значенняМ, С і МЕм":

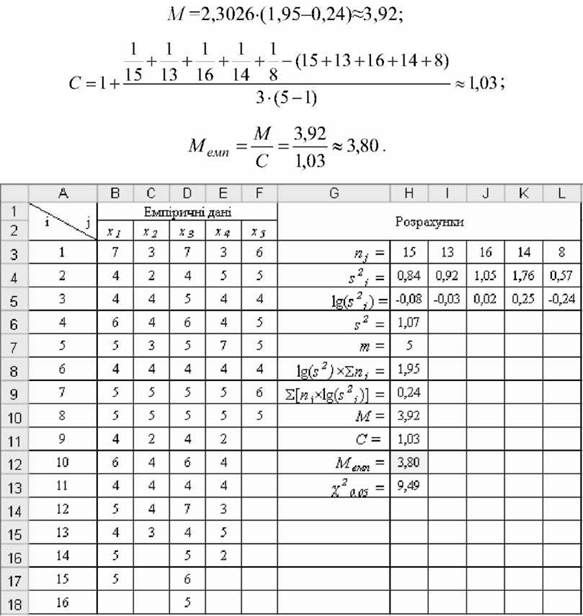
Рис. 5.41. Розрахунки критерію БартлетаМ o Визначення критичного значення критерію. Відношення МІС підкоряється розподілу Х 3 числом ступенів вільності а/=т-1. Критичне значення критерію М для а=0,05 і ¿/=5-1= 4 отримано за допомогою функції =ХИ20БР() і становить Д05 = 9,49.

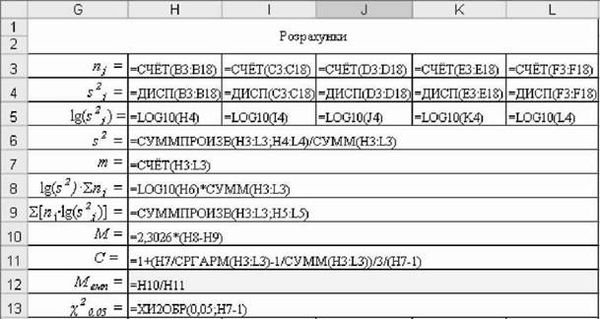
Рис. 5.42. Формули для розрахунку критерію БартлетаМ

O Прийняття рішення. Оскільки МЕм" < X о,05 нульова гіпотеза h0 приймається на рівні значущості 0,05.

O Формулювання висновків. На рівні значущості 0,05 відмінності між дисперсіями вважаються статистично незначущими.

Запитання. Завдання.

1. При яких умовах використовується z-критерій?

2. Яка ідея методу перевірки статистичних гіпотез, що використовує функцію MS Excel =ZTECT().

3. При яких умовах використовується г-критерій Стьюдента для перевірки статистичної гіпотези щодо оцінки середнього?

4. Для яких ситуацій використовується г-критерій Стьюдента, якщо необхідно оцінити істотність різниць середніх двох сукупностей?

5. Виконайте перевірку статистичних гіпотез щодо різниці середніх за допомогою пакета "Аналіз даних" розділ "Двовибірковий t-тест із різними дисперсіями".

6. Виконайте перевірку статистичних гіпотез щодо різниці середніх за допомогою функції MS Excel =ТТЕСТ().

7. Який критерій використовується для оцінки рівня дисперсії?

8. Для яких ситуацій використовується ^-критерій Фішера, якщо необхідно оцінити істотність різниць дисперсій двох сукупностей?

9. Для яких ситуацій використовується г-критерій Стьюдента, якщо необхідно оцінити істотність різниць дисперсій двох сукупностей?

10. Для яких ситуацій використовуються критерії Кохрана і Бартлета?

11. Виконайте перевірку гіпотез щодо різниці дисперсій за допомогою пакета "Аналіз даних" розділ "Двовибірковий ^-тест для дисперсій".

12. Виконайте перевірку статистичних гіпотез щодо різниці дисперсій за допомогою функції MS Excel =ФТЕСТ().

13. Повторіть математичні процедури завдань за прикладами 5.10 - 5.17.

14. Виконайте лабораторні роботи № 13 - № 17.

Схожі статті




Математична статистика - Руденко В. М. - Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Бартлета М для вибірок різних обсягів)

Предыдущая | Следующая