Математична статистика - Руденко В. М. - Коефіцієнт лінійної кореляції Персона rху

Коефіцієнти кореляції як міри зв'язку між випадковими величинами є також величинами випадковими, носять імовірнісний характер. Статистичні висновки про кореляційний зв'язок між величинами роблять не з генерального коефіцієнта кореляції р (значення цього параметра є звичайно невідомим), а за його вибірковим аналогом г. Оскільки коефіцієнти кореляції Г розраховується за значеннями змінних, які випадково потрапили у вибірку з генеральної сукупності, то й статистика г є величиною випадковою, яка потребує статистичної оцінки.. Як правило, перевіряють нульову гіпотезу про відсутність кореляційного зв'язку між змінними у генеральній сукупності, тобто Н0: р = 0. Достовірність (вірогідність) коефіцієнтів кореляції залежить від прийнятого рівня значущості а і обсягу вибірки п.

Коефіцієнт лінійної кореляції Персона rХу

Коефіцієнт кореляції гХу як вибіркова статистика є мірою оцінкою свого генерального параметра рХу. Статистика лінійного коефіцієнта кореляції має розподіл Стьюдента:

Г

Г 7(1 - Гі)/(п - 2) o (530)

Нульову гіпотезу Н0 відхиляють на рівні значущості А, якщо критичне значення г-критерію не перевищує емпіричного значення ГГ.

Приклад 5.21. Оцінити значущість кореляційного зв'язку між успішністю виконання тестових завдань з фізики (X) і математики (У) учнями загальноосвітньої школи (табл. 5.46).

Послідовність рішення:

O за емпіричними даними В2:С13 (рис. 5.46) оцінити характер лінійності зв'язку між ознаками x і У за допомогою діаграми розсіяння (рис. 5.47);

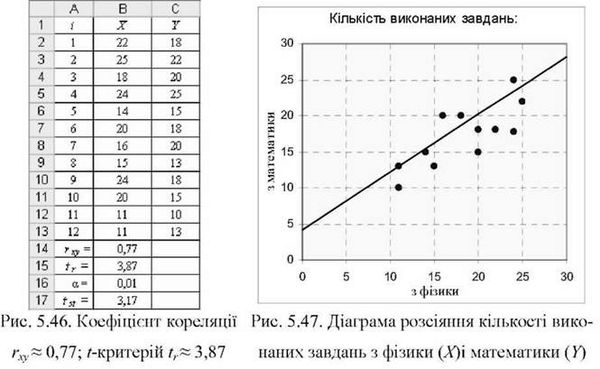
O переконатися, що кореляція лінійна. З діаграми видно, що зв'язок прямий і лінійний (рис. 5.47).Це дає підстави для застосування критерію TR для оцінювання значущості коефіцієнта кореляції Пірсона RXy;

O у комірці В14 розрахувати коефіцієнт кореляції Пірсона за допомогою функції MS Excel =nnPCOH(B2:B13;C2:C13). Значення = +0,77 свідчить про Сильний прямий зв'язок між ознакамиX і Y;

O у комірці В15 розрахувати емпіричний критерій TR за допомогою виразу =В14*КОРЕНЬ((СЧЕТ(Л2:Л13)-2)/(1-В14Л2)) і отримати значення TR~ 3,87;

O отримати однобічне критичне значення t-критерію Стьюдента за допомогою функції =СТЬЮДРАСПОБР(), яка повертає t0iOi ~ 2,76. Для цього у комірку В17 внести вираз =СТЬЮДРАСПОБР(2*В16;СЧЕТ(Л2:Л13)-2).

O Прийняття рішення: Оскільки tR >t001 (3,87>2,76), нульова гіпотеза відхиляється.

O Висновки: значення ~ +0,77, яке свідчить про Суттєвий прямий лінійний зв'язок між результатами виконання учнями тестових завдань з фізики і математики, можна вважати істотними на рівні значущості а=0,01.

Коефіцієнт рангової кореляції Спірмена rS

Коефіцієнт рангової кореляції Спірмена г8 використовується для визначення тісноти зв'язків між кількісними і якісними ознаками, якщо їх значення проранжовані. Коефіцієнт кореляції рангів г8 розраховується за формулою:

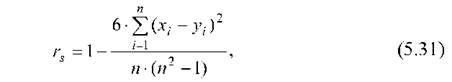
Де: П - обсяг сукупності об'єктів; (х,-у) - різниця рангів /-го об'єкта. Коефіцієнт Г8 приймає значення в інтервалі від -1 до +1.

Приклад 5.22. Оцінити наявність і значущість зв'язку між оцінками експертів толерантності студентів до викладача (змінна X) і толерантності до інших студентів (змінна У). Дані представлено в таблиці рис. 5.48.

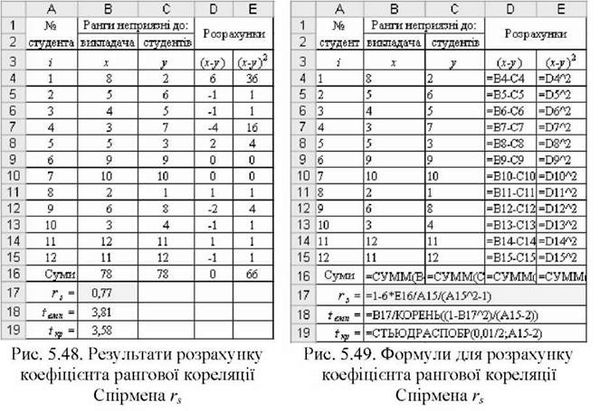
Послідовність рішення:

O Для Обчислення коефіцієнта кореляції г8 внести відповідні вирази:

- у комірку вираз =В4-С4, аналогічні вирази - у комірки Б5: Б15;

- у комірку Е4 вираз =Б4Л2, аналогічні вирази внести у комірки Е5: Е15;

- у комірку Е16 вираз =СУММ(Е4:Е15);

- у комірку В17 вираз = 1-6*Е16/Л15/(Л15Л2-1), отримати значення 0,77:

R = 1--2-" 0,77 .

S 12 o (122 -1)

O Оцінка значущості коефіцієнта рангової кореляції rS. Вибірковий розподіл rS, що характеризує нульову кореляцію між двома групами рангів, пов'язаний з t-розподілом Стьюдента. Якщо значення rS дорівнює 0 і n >10, емпіричний критерій для ступенів вільності (n-2) визначається за формулою:

R

T = S .

ЄМП І Z

V(1" rS2)/(n - 2)

У комірку В18 внести вираз: =В17/КОРЕНЬ((1-Б17Л2)/(Л15-2)), отримати значення TEMn ~ 3,81. Для малих сукупностей (n<10) перевірка нуль-гіпотези вимагає точного визначення вибіркового розподілу rS.

O Критичне значення t-критерію отримати для а =0,01 і n=15. У комірку В19 внести функцію =СТЬЮДРАСПОБР(0,01/2;Л15-2), яка дасть tKp~ 3,58.

Висновки: оскільки tEM" > tKp (3,81 >3,58), нуль-гіпотеза про відсутність кореляції відхиляється на рівні 0,01. Чисельне значення г^=0,77 свідчить про суттєвий прямий зв'язок.

Схожі статті




Математична статистика - Руденко В. М. - Коефіцієнт лінійної кореляції Персона rху

Предыдущая | Следующая