Теорія статистики - Мармоза А. Т. - 9.6. Непараметричні критерії оцінки кореляційного зв'язку

Наведені вище формули для визначення тісноти зв'язку між ознаками передбачають, що сукупності, до яких вони застосовуються, мають нормальний, або близький до нормального розподіл. Якщо ж характер розподілу досліджуваної сукупності навіть передбачувано невідомий, то тісноту зв'язку можна обчислити за допомогою непараметричних критеріїв визначення тісноти зв'язку.

Особливістю цих критеріїв є те, що тіснота зв'язку між ознаками визначається не за кількісними значеннями варіантів, а за допомогою порівняння їх рангів. Під рангом розуміють порядковий номер одиниці сукупності в ранжированому ряду розподілу. Чим менші розбіжності між рангами, тим тісніший зв'язок між ознаками.

До непараметричних критеріїв показників тісноти зв'язку відносяться коефіцієнти: кореляції рангів, знаків Фехнера, асоціації, контингенції та ін.

Коефіцієнт кореляції рангів - Це один з найпростіших показників тісноти зв'язку (його же називають ранговим коефіцієнтом кореляції Спірмена). Суть його розрахунку полягає в такому. Парні спостереження двох взаємопов'язаних ознак (результативної і факторної) ранжируються, а потім відповідно величині ознаки їм надається ранг від 1 до п. Тіснота зв'язку визначається на основі близькості рангів і формула коефіцієнта кореляції рангів буде мати вигляд:

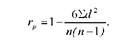
Де І - різниці між величинами рангів в порівнюваних рядах; П - число спостережень.

Смисл його такий самий як і лінійного коефіцієнта кореляції. Коефіцієнт кореляції рангів, як і лінійний коефіцієнт кореляції, може приймати значення від - 1 До + 1. Якщо ранги двох паралельних рядів повністю співпадають, то Їй = 0 І тоді має місце прямий функціональний зв'язок, а Гр = 1. При повному зворотному зв'язку (ранги розміщуються в зворотному порядку) Гр= - 1 . Ранжирувати обидві ознаки потрібно в одному і тому самому порядку: або від менших значень ознаки до більших, або навпаки.

Методику розрахунку коефіцієнта кореляції рангів покажемо на прикладі визначення тісноти зв'язку між урожайністю хмелю і кількістю внесених органічних добрив на 1 Га хмелю (табл. 9.5).

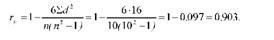
Розрахований коефіцієнт кореляції рангів свідчить про наявність прямого тісного зв'язку між урожайністю хмелю і кількістю внесених органічних добрив.

Вірогідність коефіцієнта кореляції рангів можна перевірити за таблицею Фішера (дод. 9). Табличне значення коефіцієнта кореляції при А = 0,05 і К = п - т = 10 - 2 = 8 становить гр = 0,632. Оскільки г^ВКІ > г005 (0,903 > 0,632), можна зробити висновок про те, що вибірковий коефіцієнт кореляції рангів є вірогідним.

Таблиця 9.5. Дані для розрахунку коефіцієнта кореляції рангів

дані для розрахунку коефіцієнта кореляції рангів

Недоліком коефіцієнта кореляції рангів є те, що однаковим різницям можуть відповідати зовсім відмінні різниці значень ознак (у випадку кількісних ознак). Тому для останніх слід вважати кореляцію рангів приблизною мірою оцінки тісноти зв'язку.

Коефіцієнт кореляції рангів може бути також використаний для визначення тісноти зв'язку між якісними (атрибутивними) ознаками, яким може бути надана рангова оцінка.

Коефіцієнт Фехнера Застосовується для оцінки тісноти зв'язку на основі порівнянь знаків відхилень значень результативної і факторної ознак від їх середніх, його обчислюють за формулою

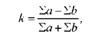
Де Еа - сума збігів знаків; ЕЬ - сума незбігів знаків.

Коефіцієнт Фехнера змінюється від 0 до ±1. Якщо знаки всіх відхилень збігаються, то ЕЬ = 0, а коефіцієнт Фехнера дорівнює одиниці, що свідчить про наявність прямого зв'язку. Якщо знаки всіх відхилень будуть різними, то Еа = 0, а коефіцієнт Фехнера дорівнює -1, що вказує на наявність оберненого зв'язку.

Розглянемо порядок обчислення коефіцієнта Фехнера на прикладі табл. 9.6.

Таблиця 9.6. Дані для розрахунку коефіцієнта Фехнера

дані для розрахунку коефіцієнта фехнера

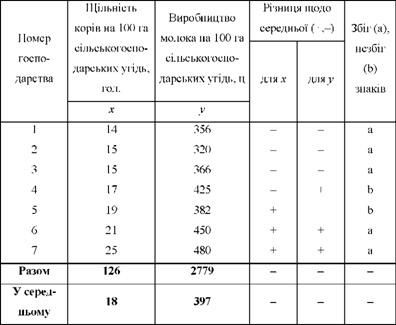
Знак мінус означає, що значення ознаки менше середньої, знак плюс - більше середньої. Збіг знаків по обох ознаках означає узгоджену варіацію, незбіг - порушення узгодженості.

Коефіцієнт Фехнера для нашого прикладу становитиме

Одержана додатна величина коефіцієнта Фехнера свідчить про те, що між виробництвом молока на 100 га сільськогосподарських угідь і чисельністю корів є прямий кореляційний зв'язок.

Слід мати на увазі, що коефіцієнт Фехнера тільки констатує наявність і напрям кореляційного зв'язку і не залежить від величини відхилень результативної і факторної ознак від відповідних середніх, у зв'язку з чим оцінка тісноти зв'язку є наближеною. Коефіцієнт Фехнера може бути деяким орієнтиром в оцінці інтенсивності зв'язку.

Тісноту зв'язку між атрибутивними (якісними) ознаками можна виміряти за допомогою спеціальних коефіцієнтів Асоціації і контингенції, Запропонованих відповідно Д. Юлом і К. Пірсоном.

Для їх обчислення будується чотириклітинна таблиця, яка показує зв'язок між двома ознаками, кожна з яких повинна бути альтернативною, тобто такою, що складається з двох якісно відмінних один від одного значень (наприклад, стан посівів задовільний або незадовільний, землі удобрені або неудобрені та ін.).

Загальна схема чотириклітинної таблиці має вигляд (табл. 9.7).

Таблиця 9.7. Чотириклітинна таблиця для розрахунку коефіцієнтів асоціації і контингенції

чотириклітинна таблиця для розрахунку коефіцієнтів асоціації і контингенції

В цій таблиці А і В ознаки, між якими вивчається зв'язок; не А і не В - протилежні (альтернативні) ознаки: а, Ь, с, сі - частоти відповідних комбінацій ознак; N - загальне число спостережень.

Коефіцієнти обчислюються за формулами:

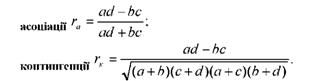
Методику розрахунку коефіцієнтів асоціації і контингенції розглянемо на прикладі визначення тісноти зв'язку між двома якісними ознаками: термінами обробки хмільників пестицидами і ступенем їх ураженості хворобами (табл. 9.8).

Таблиця 9.8. Розподіл ділянок хмільників, уражених і не уражених хворобами

розподіл ділянок хмільників, уражених і не уражених хворобами

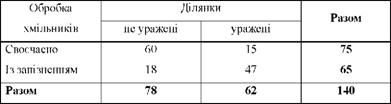
У таблиці А = 60; Ь = 15; с = 18; Сі = 47. Розрахуємо коефіцієнти

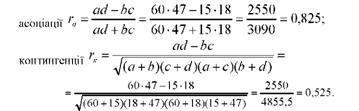
Одержані коефіцієнти асоціації і контингенції вказують на досить тісний зв'язок між термінами обробки і ураженістю хворобами хмільників.

При цьому коефіцієнт контингенції дає більш обережну оцінку тісноти зв'язку між ознаками.

Коефіцієнти асоціації і контингенції можуть приймати будь-які значення від - 1 до + 1. Коефіцієнт контингенції завжди менше коефіцієнта асоціації. Для великих вибірок (п > 30) зв'язок практично вважається

Значущим, якщо і"а > 0,5, або Ук > 0,3. Величини коефіцієнтів асоціації і контингенції, як показників тісноти зв'язку, тлумачаться так само як і величина коефіцієнта кореляції.

Схожі статті




Теорія статистики - Мармоза А. Т. - 9.6. Непараметричні критерії оцінки кореляційного зв'язку

Предыдущая | Следующая