Статистика - Опря А. Т. - § 2.7. Кластерний аналіз. Загальне поняття, його математичні основи та завдання

Як уже відомо, факторний аналіз найбільш яскраво відображує риси багатомірного аналізу в частині дослідження зв'язку між ознаками. Кластерний аналіз ці риси відображує з боку класифікації об'єктів. Сіизіег (англ.)- нагромадження груп елементів, які характеризуються якою - небудь загальною властивістю. Суть його зводиться до групування (кластеризації) сукупності з різноманітними ознаками з метою одержання однорідних груп - кластерів. При цьому межі таких груп наперед не завдані, а кількість їх може бути або завдано, або ні. Одержані в результаті розмежування групи називаються кластерами, а методи їх знаходження - кластер-аналізом. У кластерному аналізі ознаки об'єднуються в один кількісний показник схожесті (несхожесті) групуючих об'єктів.

Будь яка міра схожисті являє собою деяку функцію, яка ставить у відповідність кожній парі точок (х;, Хі) деяке ЧИСЛО СІу, що характеризує ступінь схожості (наближеності)між об'єктами И;, Практично використовується такі типи мір схожисті : 1) коефіцієнт подібності) так звані квантифіковані коефіцієнти зв'язку); 2) коефіцієнти зв'язку (кореляції); 3) показники відстані в метричному просторі.

Роль міри схожості відіграє функція відстані, введення якої веде до поняття метричного простору. Останній являє собою множину елементів з будь - якою природою явищ. Для будь - якої пари елементів цієї множини визначено певне уречевлене число, яке називається відстанню. Найбільше вживані його показники в завданнях автоматичної класифікації соціально - економічних об'єктів - це відстань по Хеммінгу та евклідова відстань.

Якщо уявити будь - яку пару елементів Е і Д, а уречевлене для них число Б (Е, Д), вкажемо три властивості відстані : 1) якщо Е і Д збігаються, відстань Б (Е, Д)= 0; 2) для будь - яких трьох точок Е, Д, С

Б (Е, Д)< Б (Е, С) (С, Д); 3) Б (Е, Д)= Б (Д, Е,).

Серед відомих функцій відстані найрозповсюдженіша - евклідова відстань. Емпірична формула її має вигляд :

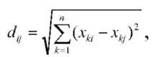
Де хкі - значення к-ої ознаки в і - му об'єкті.

Враховуючи недоліки евклідової відстані, зумовлені неможливістю врахувати можливу нерівномірність осей простору, математична література рекомендує користуватися нормованою евклідовою відстанню. Розрахунок її аналогічний розрахунку величини А4, але за стандартизованими значеннями ознак.

Необхідність такого способу розрахунку пояснюється тим, що можливий випадок, коли два об'єкти досить схожі за всіма ознаками і значно різняться за однією. За цією ознакою у евклідовій відстані вони будуть далекі одна від одної. Іншими словами, величина

Залежить від масштабу виміру ознак. Для забезпечення співставності ознак їх, як правило, нормують за середньоквадратичним відхиленням (сг). Евклідова відстань, як і аналогічні їй відстані Махаланобіса, відстань методу потенціальних функцій і т. п. прийнятна у розрахунках з ознаками, які мають кількісний вимір. Для якісних ознак, які приймають тільки два значення (о і 1), застосовують формулу відстані по Хеммінгу:

К =1

Де хк;- значення к - ої ознаки в і - му об'єкті.

Якщо ознаки класифікуються з довільним числом градацій, рекомендується використовувати формулу міри близкості двох розбивань А(Е, д), яка має властивості геометричної відстані:

Д)=2 І К* - а,* І,

2 Г, г=1

Де Ег8=1 якщо об'єкти х3, х2 знаходяться в одному класі; Ег8=0, якщо об'єкти х$, хг знаходяться в різних класах.

По розбиванню елемента Д розрахунки виконуються аналогічно ( Д,,ч 1 :Д, л 0,).

Суть завдання кластерного аналізу така: існуючу деяку множину об'єктів необхідно розділити за допомогою певного правила на раніше завдану або на завдану кількість класів. У символіці ці завдання можна сформулювати так: множину реалізацій, завданих у просторі х за допомогою вирішуваних функцій з у (за критерієм схожості), потрібно розділити на таку кількість і таких елементів алфавіту А, щоб втрати інформації не перевищували завданої величини К.

Таким чином, завдання кластерного аналізу зводиться до представлення первинної інформації у стислому вигляді без її втрати. Вирішенням такого завдання (як уже зрозуміло) проходить через класифікацію ознак (вимірів), якими характеризується кожний об'єкт. Але мова йде не про класичні принципи класифікації (наприклад, комбінаційне групування), а про принципи багатомірної класифікації. Суть її зводиться до об'єднання (класифікації) об'єктів не послідовно за окремими ознаками, а одночасно за великою чисельністю ознак. Такий набір їх створює так званий "ознаковий простір ". Кожній ознаці надається змістовність координати.

Оперуючи п ознаками, ми розглядаємо будь - який об'єкт як точку в п - мірному просторі, і завдання класифікації полягає у виявлені згущення точок (об'єктів) у цьому ознаковому просторі. Загальним для згущення точок є те, що групи (кластери) формуються на підставі "схожості" (наближення) об'єктів за великою кількістю ознак, тобто класифікація здійснюється одночасно за всім комплексом ознак, які характеризують об'єкт. При цьому жодна з ознак такого комплексу не є необхідною (або достатньою) умовою належності об'єкта до даної групи.

Формування груп об'єктів, близьких за комплексом ознак, більш ефективне у порівнянні з комбінаційним групуванням. Так, для останнього об'єкт, який має відхилення від меж групувальної ознаки (норми, характерної для даної групи за однією єдиною ознакою набору), буде виключений з групи. Легко уявити ситуацію, коли дана ознака використовується при першій градації об'єктів. У цьому випадку об'єкт може виявитися у групі досить віддаленої від тієї, з якою вона (ознака) має найбільшу схожість. У комбінаційному групуванні самі групи являють собою ні що інше як сектори ознакового простору. Здійснюючи класифікацію за названим групуванням, ми інколи штучно руйнуємо ознаковий простір завданими границями інтервалів груп, тоді як реально існують відокремлено однорідні класи.

Перевага методу кластерного аналізу в тому, що його математичний апарат дозволяє знайти і виділити реально існуюче в ознаковому просторі нагромадження об'єктів (точок) на підставі одночасного групування за великою кількістю ознак.

Кластерний аналіз, як і кореляційно - регресійний, є математичним апаратом вивчення статистичних зв'язків. Це метод пошуку емпіричних закономірностей, але для більш широкого класу зв'язків. Для регресійного аналізу є цілий ряд важко виконуваних умов (вимог) його застосування. Серед них вимоги нормальності багатомірного розподілу, неможливість використання якісних ознак, обмеження, які накладаються на алгебраїчну форму зв'язку (метод найменших квадратів ефективний для лінійних рівнянь ) і ін.

Для методу кластерного аналізу однорідність сукупності не є обов'язковою умовою. Більше того, сам метод дозволяє виявити і описати структурні закономірності, забезпечивши формування однорідних класів об'єктів. Дискретність кластерних моделей на відміну від неперервних регресійних моделей, зумовлена усередненням і деякими втратами інформації, забезпечує більш евристичний характер обчислювальних процедур, а також знімає обмежування, пов'язані з алгебраїчною формою зв'язку.

Нарешті, комплексне використання обох методів у вивченні статистичних зв'язків створює умови широкого використання методу кореляційно - регресійного аналізу, забезпечуючи умови для адекватного його додатка.

Викладене вище дає змогу зробити висновок про те, що застосуванню методу кластерного аналізу повинно передувати вивчення теорії і накопиченої практики цього використання. На початкових етапах використання цього методу дослідник повинен мати чітко уявлення, яке з двох завдань він вирішує. Чи це звичайне завдання типізації, при якому досліджувану сукупність спостережень слід розділити на відносно невелику кількість групувань. Тоді виконується робота, аналогічна одержанню інтервалів статистичного групування при обробці одномірних спостережень. При цьому операція здійснюється так, щоб елементи однієї області групування знаходились один від одного по можливості на невеликій відстані. Друге завдання може полягати в тому, що дослідник намагається визначити природну відстань вихідних елементів (спостережень) на чітко виражені кластери, що знаходяться один від одного на деякій відстані, але які не розбиваються на такіж віддалені одна від одної частини. Слід пам'ятати, що перше завдання ( завдання типізації) завжди має рішення, друге - в своїй постановці може мати негативний результат, тобто може виявитися, що множина вихідних спостережень не виявляє природного розташування на кластери, наприклад, утворює один кластер.

Досить важливим етапом кластер - аналізу є вибір змінних (ознак). Ця стадія аналізу є основою формування однакових просторів, у яких повинно проводитися моделювання.

Вибір ознак здійснюється, як правило, у дві стадії. В основі першої з них лежить формування первинної гіпотези про набір ознак, які впливають на досліджуване явище; в основі другої - уточнення гіпотези по результатах консультацій (опитувань) спеціалістів досліджуваної галузі.

Завершеною вважається економічна постановка завдання при умові її узгодженості з вимогами використовуваного математичного апарату і можливостями обчислювальної техніки. Після цього приступають до збору вихідної інформації.

Схожі статті




Статистика - Опря А. Т. - § 2.7. Кластерний аналіз. Загальне поняття, його математичні основи та завдання

Предыдущая | Следующая