Математична статистика - Руденко В. М. - Точково-бісеріальний коефіцієнт кореляції rpb

Для визначення тісноти зв'язку ознак X і Y, які оцінюються у двох значеннях 1 і 0, застосовується коефіцієнт <р Пірсона:

Я>= І, (5.32)

JpX ■ PY ■ (N - PX ) o (N - PY )

Де: PXy - число об'єктів, що мають "1" і з X, і з Y; PX і pY - число об'єктів, що мають "1" з XІ з YВідповідно; n - загальна кількість об'єктів.

Приклад 5.23. Оцінити зв'язаність між захопленістю учнів спортом та їхньою схильністю до математики. У таблиці рис. 5.50 позначення для X і Y: 1 - наявність ознаки, 0 - її відсутність.

Послідовність рішення:

O Розрахунки коефіцієнта <р проводимо за допомогою таких виразів:

- у комірку В15 внести вираз =СЧЕТ(В3:В14);

- у комірку В16 - вираз =СУММЕСЛИ(В3:В14;"=1";С3:С14);

- у комірку В17 - вираз =СУММ(В3:В14);

- у комірку В18 - вираз =СУММ(С3:С14);

- у комірку В19 - вираз =(В15*В16-В17*В18)/КОРЕНЬ(В17*В18*(В15-В17)*(В15-В18)). Звичайні арифметичні розрахунки дають аналогічний результат коефіцієнта кореляції <р Пірсона длярХу = 5,рХ = 6, рУ = 7 і п = 12:

12o5 - 6 o 7 У> = ~ 0,51.

Д/6 o 7 o (12 - 6) o (12 - 7)

O Оцінка значущості коефіцієнта кореляції ^. Якщо прийняти, що вибірковий розподіл коефіцієнта ер приблизно описується нормальним законом з нульовим середнім і одиничним стандартним відхиленням, перевірка нуль-гіпотези виконується за допомогою г-критерію: гЕмп = д) -4п.

Внести у комірку В20 вираз =В19*КОРЕНЬ(В15) і отримати 2Емп:

ІЕяп = 0,51 -712 * 1,76.

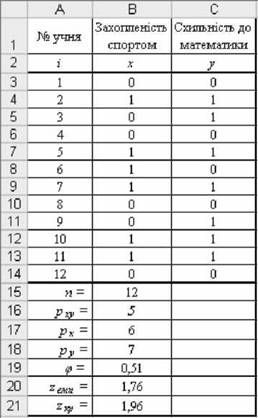
Рис. 5.50. Розрахунки коефіцієнта кореляції <р

O Критичне значення г-критерію для а=0,05 розташоване нижче гО/2 стандартного нормального розподілу (0,025 або 0,975). У комірку В21 внести функцію =НОРМСТОБР(1-0,05/2), яка поверне значення гКр ~ 1,96.

Висновки: оскільки гЕм"<іКр (1,76<1,96), на рівні значущості 0,05 нульова гіпотеза Н0 приймається. Отже, значення коефіцієнта Ер ~ 0,51 не може свідчити про існування зв'язку між захопленістю спортом учнів і проявом схильності до математики.

Точково-бісеріальний коефіцієнт кореляції rpb

Точково-бісеріальний коефіцієнт кореляції гРЬ використовується для емпіричних даних, значення яких отримано за різними шкалами вимірювань, наприклад, якщо змінна X вимірюється за дихотомічною шкалою, а змінна У - у шкалі інтервалів або відносин:

_ У1 - У 0 І п1 ■ п0 ГРь - Лі : тг, (5.33)

*у п ■ (п -1)

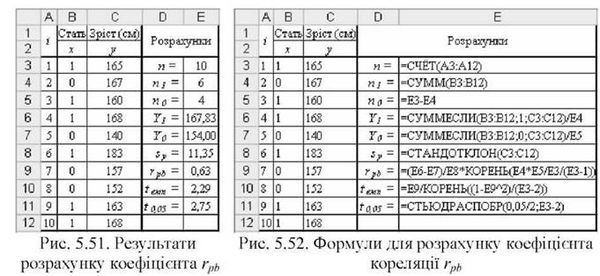
Де У1 і п1- середнє і кількість У об'єктів, що мають 1 з X; У0 і п0 - середнє і кількість У об'єктів, що мають 0 з X; яУ - стандартне відхилення всіх П значень У; П = п1 + п0 . Приклад 5.24. Оцінити зв'язок між показниками "стать" і "зріст" рис. 5.51 для 15 підлітків (x = 1 для чоловічої, x = 0 для жіночої статі). Послідовність рішення:

O Розрахунки коефіцієнта кореляції гРЬ :

- у комірку Е3 внести =СЧЕТ(Л3:Л12) і отримати п = 10;

- у комірку Е4 внести =СУММ(В3:В12) і отримати п1=6;

- у комірку Е5 внести =Е3-Е4 і отримати п0=4;

- у комірку Е6 внести =СУММЕСЛИ(В3:В12;1;С3:С12)/Е4 і отримати середній зріст хлопчиків У1 "167,83 см;

- у комірку Е7 внести =СУММЕСЛРІ(В3:В12;0;С3:С12)/Е5 і отримати середній зріст дівчат У0 ~ 154 см;

- у комірку Е8 внести =СТАНДОТКЛОН(С3:Є12) і отримати стандартне відхилення 5У= 11,35;

- у комірку Е9 внести вираз для розрахунку точково-бісеріального коефіцієнта =(Е6-Е7)ІЕ8*КОРЕНЬ(Е4*Е5ІЕ3І(Е3-1)) і отримати його значення:

= 167,83-154 Р^ Т 0,63

РЬ 11,35 10 o (10-1) ■

На рис. 5.51 представлено результати розрахунку точково-бісеріального коефіцієнта кореляції г"Ь, на рис. 5.52 - відповідні розрахункові формули.

O Оцінка значущості коефіцієнта кореляції гРЬ зводиться до перевірки нуль-гіпотези (Н0: гРЬ = 0) , для якої використовується статистика г-критерій Стьюдента з (п-2) ступенями вільності:

Г = , І* . (5.34)

^/(1 - гД )І(п - 2) ' '

Для розрахунку гЕля у комірку Е10 внести =Е9ІКОРЕНЬ((1-Е9Л2)І(Е3-2)) і отримати значення гЕля ~ 2,29.

O Критичне значення г-критерію можна отримати за допомогою функції =СТЬЮДРАСПОБР(<хІ2; п-2). При а =0,05 і п=10 у комірку В256 внести функцію =СТЬЮДРАСПОБР(0,05І2;Е3-2), яка дає значення г", = 2,75.

O Висновки: оскільки отримане значення ЇЕмп -2,29 не перевищує критичне значення ^-2,75 нуль-гіпотеза про відсутність кореляції приймається. Отже, з імовірністю 95% (а=0,05) правдоподібно, що у цій ситуації коефіцієнт кореляції гРЬ, який приймає доволі суттєве значення (0,63), не є вірогідним!

Запитання. Завдання.

1. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості коефіцієнта лінійної кореляції Пірсона.

2. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості коефіцієнта рангової кореляції Спірмена.

3. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості дихотомічного коефіцієнта кореляції Пірсона ^.

4. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості точково-бісеріального коефіцієнта кореляції.

6. Повторіть математичні процедури завдань за прикладами 5.21 - 5.24.

7. Виконайте лабораторні роботи № 20 - № 22.

Схожі статті




Математична статистика - Руденко В. М. - Точково-бісеріальний коефіцієнт кореляції rpb

Предыдущая | Следующая