Статистика - Опря А. Т. - § 1.4. Перевірка статистичних гіпотез відносно розподілів

Серед статистичних характеристик, відносно яких може висуватися і оцінюватися гіпотеза, найважливішим параметром є середня величина. Це зумовлює її роль як основної узагальнюючої характеристики статистичної сукупності.

Задачі, пов'язані з оцінкою гіпотез про середні величини, поділяються на дві групи: 1) дисперсія вихідної (генеральної) сукупності відома; 2) дисперсія вихідної сукупності невідома. При невідомій величині дисперсії її заміняють дисперсією вибіркових даних (о-2).

Гіпотези відносно середніх перевіряються відповідно до логічних принципів у викладеній вище послідовності.

Приклад 1 (дисперсія відома). При вибірковому обстеженні 25 Голів молодняка великої рогатої худоби встановлено, що середньодобовий приріст ваги однієї голови становить 888 Г (~). Припустивши, що дані приросту розподіляються нормально з а = 30Г, перевірити на рівні значимості А = 0,05 нульову гіпотезу Н0: ХН = 900 Г Проти конкуруючої гіпотези Н : хТ ф 900 Г.

Рішення. Оскільки середньоквадратичне відхилення відомо, знаходимо

Спостережене значення вибіркової характеристики - Розрахункове (Хр):

Г Х - ~Н0 Г 888 - 900 г - 2

Оскільки конкуруюча гіпотеза Н : ~Н1 ф 900 г, вибираємо двосторонню критичну область з границями, які обчислюються із умови ї (ї) = 1-а = 0,95.

За стандартною таблицею значень функції Лапласса (додаток 5). знаходимо, що рівню ймовірності Р= 0,95 відповідає табличне |ї|=1,96.

Оскільки |їР| > їт (|2| >1,96), нульова гіпотеза (Н0) відхиляється, тобто вона протирічить вибірковим даним. Робимо висновок, що середньодобовий приріст ваги однієї голови молодняка тварин суттєво відрізняється від показника 900 г.

Приклад 2 (дисперсія невідома). При вибірковому обстеженні 10 голів молодняка тварин встановлений добовий приріст відповідно 850, 900, 910, 970, 825, 815, 827, 833, 912, 928 г.

Припустивши, що дані добових приростів ваги розподіляються нормально, необхідно перевірити на рівні значимості а = 0,05 нульову гіпотезу Н0 : ~Н0 = 850 г при конкуруючій гіпотезі Н: ~Н1= 870 г.

Рішення. Визначаємо вибіркову середню арифметичну ~ І дисперсію

А1.

~ 850 + 900 + 910 + 970 + 825 + 815 + 827 + 833 + 912 + 928 Опп

Х =-=877 г.

10

Розраховуємо дисперсію, побудувавши допоміжну таблицю 97 .

Таблиця 97

Розрахунок дисперсії

Х1 - X

(х, - Х)2

850

-17

289

900

33

1089

910

43

1849

970

3

9

825

-42

1764

815

-62

2704

827

-40

1600

833

-34

1156

912

45

2025

928

61

3721

8770

X

16206

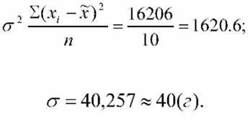
Оскільки відповідно умови і задачі дисперсія генеральної сукупності

Невідома, число ступенів вільності дорівнює у = п -1. Розрахункове значення

Нормованого відхилення знаходимо за формулою:

Х - ~н0 /-Г 877 - 850 [-- " "" ,

ГР =--V п -1 =-л/10 -1 = 2.02. У зв'язку з тим, що

(Я1:3сН1 = 870 > ЗсН0) рівно як і для (Я1:3сН1 < ~Н0) вибираємо односторонню критичну область, границі якої обчислюємо з умови /(г) = 1 - 2А = 1 - 2 Х 0.05 = 0.90.

За стандартною таблицею г - розподілу (див. додаток. 1) для числа ступенів вільності У = 10 - 1 і рівня значимості а = 2 х 0,05 (0,10) знаходимо ХТ =1,83. Оскільки |гР| >гТ (|2,02| > 1,83), нульова гіпотеза відхиляється, тобто вона протирічить вибірковим даним. Робимо висновок, що середньодобовий приріст однієї голови суттєво відрізняється від 850 г.

§ 1.4. Перевірка статистичних гіпотез відносно розподілів

Розглянуті раніше питання перевірки статистичних гіпотез торкались величин параметрів досліджуваних статистичних сукупностей. При цьому міркування велись, виходячи з передбачень про однорідність сукупності і нормальності розподілу її одиниць. Тобто, сукупності що досліджуються, типові і різняться лише розмірами рівнів досліджуваних ознак. Але окремі випадки вимагають обов'язковості перевірки гіпотези відносно характеру розподілу. Тут необхідно вирішувати такі завдання:

1. Визначити відповідність емпіричного розподілу тому чи іншому теоретичному виду розподілу - нормальному, біноміальному, поліноміальному і т. п.

2. Визначити можливість належності двох і більше емпіричних розподілів до одного і того ж виду розподілів.

3. З'ясувати наявність незалежності у розподілі ознак однієї від іншої.

При перевірці гіпотез про розподіли широке застосування

Знаходить Хі - квадрат критерій. Детальне викладення аспектів і умов його використання буде дано нижче.

Оскільки емпіричний розподіл не завжди цілком відповідає нормальному розподілу, часто потрібно з'ясувати, сильно чи слабо розходяться емпіричні і теоретичні ряди. З цієї метою, необхідно встановити таку границю, недосягнення якої означає, що розбіжність між емпіричним і нормальним розподілом ще не така велика, щоб її враховувати, і що даний емпіричний ряд ще можна практично прийняти за нормальний. З цієї метою розраховується критерії Хі-квадрат (Х2 ),

Величина х1 визначається за уже відомою формулою:

П (п, - пТ )2 .

Х2 = 2---,Де Пф пт - відповідно частоти емпіричного і

Теоретичного ряду.

Як бачимо, критерій Хі - квадрат являє собою суму відношень між квадратами різниць емпіричних і теоретичних частот до теоретичних частот.

Якщо при вибраному рівні ймовірності обчислені значення Х2 перевищують табличні, то нульова гіпотеза про відповідність емпіричного розподілу теоретичному відхиляється.

Приклад. Розглянемо випадок перевірки статистичної гіпотези про відповідність емпіричного розподілу нормальному. Для прикладу використаємо ряд розподілу підприємств за показником собівартості виробництва однієї деталі (табл. 98).

Емпіричний розподіл представлено у вигляді інтервального ряду. Він заданий послідовністю рівновіддалених варіант (центр інтервалу) і відповідних частот.

Потрібно, використовуючи критерій х2 ,перевірити гіпотезу про те, що генеральна сукупність Х розподілена нормально.

Для того, щоб при заданому рівні значимості а перевірити гіпотезу про нормальний розподіл генеральної сукупності, необхідно виконати обчислювальну роботу за такими етапами:

1. Обчислити вибіркову середню ~ і вибіркове середнє квадратичне відхилення А.

2. Обчислити теоретичні частоти

ПТ = /(ї) х -, а

Де П - чисельність вибірки (сума всіх частот), ХІ = ~ |

Ї - шаг інтервалу ї =-,

Ег

1 -'- . . .

/= -[2~ПЄ 2 (СпецІАльнІ таблиці - координати кривої).

Таблиця 98

Розрахунок частот нормального розподілу( вирівнювання емпіричних частот за нормальним законом)

Інтервал собівартості однієї деталі, грн. 0=9)

Середине значення /центр/ інтервалу,

Х1

Число підприємств,

П І

Розрахункові величини

Статистичні параметри

ХІ ПІ

XT-x

(x¡- х)2

(x¡- х)2Щ

Нормоване відхилення, ХІ ~ Х 1 а

Табличне значення функції

Fifi *

Теоретична

Частота нормального ряду розподілу

Г, Ч ПІ

/0)х - А

Округлене значення теоретичної частоти,

ПТ

67-76

72

3

216

-28

784

2352

2,15

0,0395

1,81

2

76-85

81

5

405

-19

361

1805

1,46

0,137

6,26

6

85-94

90

15

1350

-10

100

1500

0,77

0,297

13,57

14

94-103

99

16

1584

- 1

1

16

0,08

0,398

18,19

18

103-112

108

17

1836

8

64

1088

0,62

0,329

15,04

15

112-121

117

7

819

17

289

2023

1,31

0,169

7,72

8

121-130

126

2

252

26

676

1352

2,00

0,054

2,47

2

130-139

135

1

135

35

1225

1225

2,69

0,011

0,50

1

Всього

X

66

6597

X

X

11361

X

X

65,56

66

2

Знаходимо за стандартною таблицею /(*) = -/=е 2 (ординати нормальної кривої додаток 3)

-¡1

Наприклад, t=2,15. Знаходимо у таблиці "2,1" на впроти "5" (0,0395).

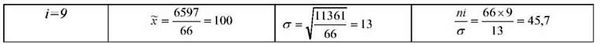
3. Співставити емпіричні і теоретичні частоти за допомогою критерію Пірсона. Для цього необхідно :

А) скласти розрахункову таблицю (див. табл. 99), за якою знайти спостережуване значення критерію:

І=1 пТ

Таблиця 99

Розрахунок значення критерію Х2

Серединне значення (центр) інтервалу

Частоти

Розрахункові величини

Емпіричне, пІ

Теоретичне, пТ

ПІ - пТ

(п; - пТ )2

ПТ

72

3

2

1

1

0,50

81

5

6

-1

1

0,17

90

15

14

1

1

0,07

99

16

18

-2

4

0,06

108

17

15

2

4

0,27

117

7

8

-1

1

0,12

126

2

2

0

0

0,00

135

1

1

0

0

0,00

Всього

66

66

X

X

1,19

А = 0,05;0,01;0,001; у = 5; % = 1,19; у2 = 11,1; У2 = 15,1; У2 = 20,5;

/І Т(0,05;5) /І Т(0,01;5) /І Т(0,001;5)

Б) за таблицею стандартних значень х2 ПРИ заданому рівні значимості А і числі ступенів вільності У = І - 3 (/ - кількість груп), знаходимо критичну точку ^2(аі. у) правосторонньої критичної області.

Якщо % < %Т, то гіпотеза про нормальність розподілу генеральної

Сукупності не відхиляється, тобто емпіричні і теоретичні частоти розрізняються

22

Незначимо (випадково). При % > ^ - гіпотезу відхиляють, тобто емпіричні і

Теоретичні частоти різняться значимо.

Нечисленні частоти (п<5 ) рекомендується об'єднувати. Відповідні їм теоретичні частоти підсумовують. За такої операції число ступенів вільності розраховують виходячи з того, що І дорівнює числу груп, які залишились після об'єднання частот.

Потрібно пам'ятати, що при перевірці гіпотези про нормальний розподіл генеральної сукупності за допомогою критерію х2 число ступенів вільності (і)) знаходять за формулою і) = І - 1 - р, де р - число параметрів, які оцінюються за вибіркою. Нормальний розподіл визначається двома параметрами: математичним очікуванням А - і середнім квадратичним відхиленням ст. Оскільки обидва ці параметри оцінювалися за вибіркою (за оцінку приймають вибіркову середню ~, , а за оцінку ст - вибіркове середнє квадратичне відхилення), то р =2, тоді, і) = (І - 1 - 2) = 1 - 3.

Виконуючи розрахунки відповідно вказаній вище послідовності, необхідно побудувати розрахункові таблиці /див. табл. 38, 39/ і обчислити всі необхідні параметри для перевірки статистичної гіпотези про відповідність

2

Емпіричного розподілу нормальному. Із таблиці 39 знаходимо У/ = 1,19.

За стандартною таблицею критичних значень розподілу %2 (див. додаток. 7), при рівні значимості а = 0,05 і числу ступенів вільності і) = І-3= 8- 3=5,

2

Знаходимо критичну точку правостороньої критичної області ^(0 05 5)= 1 1 , 1.

Оскільки % < ^ - гіпотеза про нормальний розподіл генеральної

Сукупності не відхиляється, тобто емпіричні і теоретичні частоти розрізняються незначимо (випадково).

Таким чином, висунута гіпотеза приймається. Графічне зображення розподілу емпіричних і теоретичних частот показано на рисунку 42.

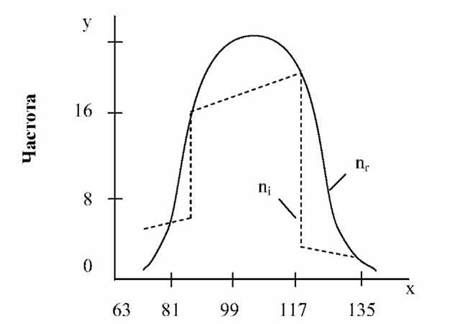
Варіанта

Рис. 42. Розподіл емпіричних (и,) і теоретичних (ПТ ) частот

Схожі статті




Статистика - Опря А. Т. - § 1.4. Перевірка статистичних гіпотез відносно розподілів

Предыдущая | Следующая