Логіка - Мозгова Н. Г. - 3. Розділово-категоричні виводи

А) Суто розділові.

Суто розділовим умовиводом с вивід, в якому всі засновки та висновки с розділовими (диз'юнктивними) висловлюваннями.

Наприклад:

Порівнянні поняття бувають сумісними (А) та несумісними (В). Несумісні поняття бувають співпідпорядкованими (В,), або протилежними (В,), або суперечними (Вя)._

Порівнянні поняття бувають сумісними (А), або співпідпорядкованими (В,), або протилежними (В2), або суперечними (В3). Структура цього виводу є такою: А або В.

В,, або В?, або Вг_

А, або В,, або В2, або В

Це правильна структура виводу і відповідна їй формула логіки висловлювань є законом логіки:

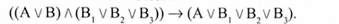
Б) Заперечно-стверджувальний модус.

Умовивід, в якому один Ь засновків з розділовим судженням, а другий - категоричним судженням, називають * розділово-категоричним. Наприклад:

Мені могли телефонувати Микола (А) або Петро (В).

Микола мені не телефонував (~А).

Мені телефонував Петро (В).

Структура цього умовиводу така:

А або В.

Не А.

В.

Відповідна їй формула логіки висловлювань:

Як бачимо, це - закон логіки, тобто правильна структура виводу. Різновидами нього виводу є такі:

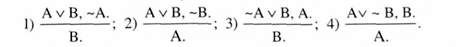
Усі ці структури і відповідні їм формули логіки висловлювань є законами логіки.

Оскільки в цих виводах ідуть від заперечення однієї альтернативи до ствердження іншої, то цей вивід називають заперечно-стверджувальним модусом (modus tullendo ponens) розділово-категоричного виводу.

У наведеному прикладі сполучник "або" ми використали в значенні "і/або", тобто альтернативи не виключали одна одну (диз'юнкція). Якщо сполучник "або" використати в суто роз'єднувальному значенні (сильна диз'юнкція), то ці структури будуть теж правильними. Наприклад:

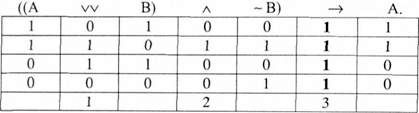
Таким чином, у виводах за modus tollendo ponens смисл сполучника "або" не має жодного значення. Тобто, якщо в наведених структурах виводу знак "V", замінити на "W", то ці структури і відповідні їм формули теж будуть законами логіки.

При виводах за структурою modus tollendo ponens обмежуючою умовою необхідного виводу є така: в розділовому засновку необхідно врахувати всі можливі альтернативи. Якщо не дотримуватися цієї умови, то висновок буде лише ймовірним.

С) Стверджувально-заперечний модус.

Наше міркування можна побудувати так:

Мені могли телефонувати Микола (А) або Петро (В).

Мені зателефонував Микола (А).

Петро мені не телефонував (~В).

Структура цього умовиводу така:

А або В.

А._

Не В.

Відповідна їй формула логіки висловлювань:

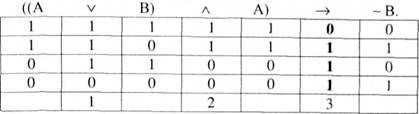
Ця формула не є завжди істинною (не є законом логіки). Отже, відповідна їй структура виводу є неправильною, тобто вона не завжди дає істинні висновки. В чому помилка? Справа в тому, що альтернативи "А або В" не виключають одна одну.

При ствердженні однієї альтернативи і запереченні (у висновку) іншої необхідно, щоб вони виключали одна одну. Тобто сполучник "або" слід використовувати в суто розділовому смислі, що відповідає логічній операції сильної диз'юнкції. Наприклад:

Мені могли телефонувати або А, або В.

Мені зателефонував В.

А мені не телефонував.

Структура цього виводу:

А МВ.

В._

-А.

Його формула:

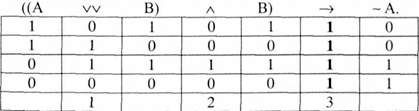
Ця структура виводу є правильною, а відповідна їй формула логіки висловлювань є законом логіки. Перехід від ствердження однієї альтернативи до заперечення іншої називають стверджувально-заперечним модусом (modus роп endo tollen s) розділово-категоричного виводу.

Різновидами цього модусу є такі:

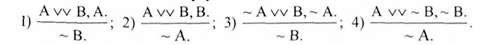
Отже, виводи за modus ponendo tollem будуть правильними, якщо розділовий засновок є сильною диз'юнкцією. Виводи стверджувально-заперечного типу з диз'юнктивним засновком є ймовірними.

4. Умовно-розділові виводи

* Умовно-розділовий умовивід - це вивід, в якому один із засновків складається з двох і більше умовних висловлювань, а інший засновок є розділовим судженням. Цей вид умовиводів називають ще лематичними (від грецького - припущення, засновок.).

У залежності від кількості умовних та розділових суджень - засновків розрізняють дилеми (від грецького - подвійний засновок), які мають два умовних засновки, та полілеми (від грецького - багато засновків), які мають більше двох умовних засновків. Найбільш типовою та поширеною формою лематичних умовиводів є дилема. У залежності від якості висновку дилеми поділяють на конструктивні та деструктивні.

А) Конструктивна дилема.

У конструктивній дилемі висновок є стверджувальним. Залежно від структури конструктивна дилема буває простою та складною.

Проста конструктивна дилема - це умовивід, у першому засновку якого формулюються дві різні підстави, з яких випливає один і той самий наслідок. У другому засновку, який є диз'юнктивним судженням, стверджується можлива істинність однієї з підстав, зазначеної у більшому засновку, а у висновку стверджується наслідок. Наприклад:

Якщо людина вивчала англійську мову (А), то вона володіє нею (В). Якщо людина жила в англомовному середовищі (С), то вона володіє англійською мовою (В).

Ця людина вивчала англійську (А) або жила в англомовному середовищі (С).

Ця людина знає англійську мову (В). Структура цього міркування є такою:

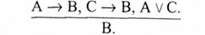
Відповідною їй формулою логіки висловлювань є така:

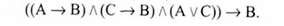
Ця структура виводу є правильною, а формула - законом логіки (завжди істинною формулою). Замість змінних (А, В, С) ми можемо поставити будь-які істинні висловлювання і висновок завжди буде істинним.

Складна конструктивна дилема - це умовивід, в умовних засновках якого з двох різних підстав випливають два різних наслідки; в диз'юнктивному засновку стверджується істинність принаймні однієї з підстав, а у висновку - істинність принаймні одного з наслідків. Наприклад:

Якщо він вивчав англійську (А), то знає її (В).

Якщо він вивчав німецьку (С), то знає її (Б).

Але він вивчав англійську (А) або німецьку (Р).

Він знає англійську (В) або німецьку (О).

Структура цього виводу така:

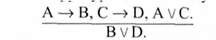
Відповідна їй формула логіки висловлювань:

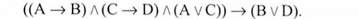
Як бачимо, складна конструктивна дилема відрізняється від простої лише тим, що з різних підстав випливають два різні наслідки. Структура цього виводу є правильною, а відповідна їй формула - тавтологією.

Б) Деструктивна дилема.

У деструктивній дилемі висновок є заперечним. Залежно від структури деструктивна дилема буває простою та складною.

Проста деструктивна дилема - це умовивід, в умовних засновках якого з однієї підстави випливають два різні наслідки; в розділовому засновку заперечуються ці наслідки; а у висновку заперечується підстава. Наприклад:

Якщо буде вільний час (А), то сходжу в кіно (В).

Якщо буде вільний час (А), то поспілкуюсь із друзями (С).

Але в кіно не сходив (~В^ або з друзями не зустрівся (~С).

Вільного часу не було (~А).

Структура цього умовиводу така:

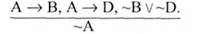
Відповідна їй формула логіки висловлювань:

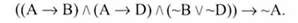
Така структура виводу є правильною, а формула - завжди істинною.

Складна деструктивна дилема - це умовивід, в умовних засновках якого з двох різних підстав випливають два різні наслідки; заперечуючи ці наслідки в розділовому засновку, переходять до заперечення цих підстав у розділовому висновку.

Наприклад:

Якщо буде мороз (А), то піду на ковзанку (В). Якщо буде відлига (С), то піду в кіно (О). Але не пішов на ковзанку (~ В) або не пішов у кіно (~ Р). Не було морозу (~ А) або не було відлиги (~ С). Структура цього умовиводу така:

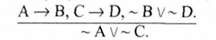
Відповідна їй формула логіки висловлювань:

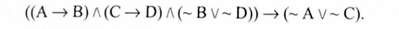
Якщо в чотирьох згаданих типах дилем диз'юнкцію в засновках та висновках замінимо на сильну диз'юнкцію, то отримані структури виводу і відповідні їм формули теж будуть законами логіки. Розділовий засновок лематичного умовиводу повинен містити в собі всі можливі альтернативи; в дилемі дві альтернативи повинні вичерпувати всі можливі випадки, інакше вивід не буде необхідним.

Схожі статті




Логіка - Мозгова Н. Г. - 3. Розділово-категоричні виводи

Предыдущая | Следующая