Логіка - Мозгова Н. Г. - 5. Відношення логічного слідування
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або тавтологіями.
Прикладом тавтології є відомий вже вам закон виключеного третього - А V - А. Побудуємо його матрицю:

Як бачимо, незалежно від того, які значення істинності мають атоми (А, - А), формула в цілому має значення істинності - "Істина" (1).
Зазначимо, що будь-який закон логіки є тотожно істинною формулою або тавтологією.
*Дві формули F1 та F2с еквівалентними (рівносильними) тоді і тільки тоді, коли їх подвійна імплікація (F1-F2) - тавтологія.
Перевірку еквівалентності двох формул здійснюють за допомогою таблиць істинності. Якщо значення їх істинності в цілому однакові, то відповідні формули еквівалентні. Перевіримо, наприклад, чи еквівалентні такі формули:
А->Ві~А УВ
Побудуємо їх таблиці істинності:
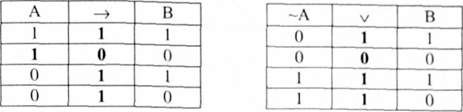
Очевидно, що подвійна імплікація цих формул є тавтологією:
(А -> В) <-* (~ А V В)
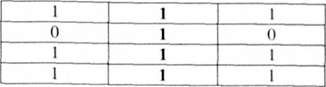
Деякими елементарними еквівалентностями логіки висловлювань є такі:
1) А->В = ~А/В - вираження імплікації через диз'юнкцію та заперечення.
2), а) ~ (А Л В) = ~ А V - В;
Ь) ~(А/В) = ~АЛ~В - закони де Моргана.
3) А <-> В = (А -> В) Л (В -> А) - подвійна імплікація через імплікацію та кон'юнкцію.
4) Скориставшись еквівалентністю (1), отримаємо: А <-> В = (~А V В) Л (~В V А).
5) Скориставшись правилом де Моргана (2Ь), отримаємо: А <-> В н ~ (А Л ~В) Л ~(В Л - А).
Відношення еквівалентності дозволяє перетворювати одні (складні) висловлювання на інші (прості).
4. Особливості імплікації
Імплікація двох висловлювань (А та В) суттєво відрізняється від інших логічних операцій - кон'юнкції, диз'юнкції та подвійної імплікації. Якщо АЛВ = ВЛА, АУВ а ВуА, А<->В = В<->А, то А->В Ф В->А. Тобто, якщо всі логічні операції є симетричними, то імплікація не є симетричною операцією.
Саме тому, ми давали її визначення не через випадок істинності, а через випадок хибності.
Тепер розглянемо випадки її істинності. Матриця імплікації має вигляд:
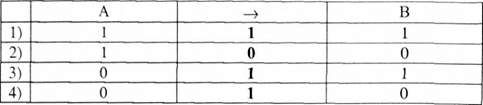
З таблиці видно, що:
1) Імплікація є завжди істинною, при хибному антецеденті, незалежно від значення істинності консеквента (рядки таблиці 3,4). В обох випадках А є хибним, але в третьому рядку В є істинним, а в 4-му В - хибне. Отже, ми можемо визначити істинність імплікації, знаючи тільки значення істинності лівої частини. Якщо вона хибна, то імплікація є істинною.
2) Імплікація є завжди істинною при істинному консеквенті (1, З рядки), незалежно від значення істинності антецедента. Так, у першому рядку він істинний, а в третьому - хибний. Це теж дозволяє визначати істинність імплікації тільки за значенням істинності консеквента.
Отже, імплікація є істинною тоді і тільки тоді, коли антецедент є хибним або консеквент є істинним.
5. Відношення логічного слідування
Дуже важливим у логіці висловлювань (і в логіці взагалі) є відношення логічного слідування, оскільки на ньому грунтуються всі умовиводи та доведення. Відношення логічного слідування позначають символом К Формула Б. н Б2 читається: "З Р. логічно слідує (випливає) Р2, або Р2 є логічним наслідком
З формули Р1 логічно слідує формула Р2 тоді і тільки тоді, коли їх імплікація (¥ ] - є завжди істинною формулою (* та етологією).
Між відношенням логічного слідування (Н) та імплікацією (->) існує тісний зв'язок, але їх не слід плутати. Імплікація - це висловлювання, що складається з двох елементарних висловлювань і серед наборів її значень істинності може бути "хиба". *Логічне слідування - це відношення між двома висловлюваннями, яке є завжди істинною імплікацією.
Для перевірки, чи є Б2 логічним наслідком ¥г необхідно:
1) з'єднати їх знаком імплікації (Р,-"Р2);
2) побудувати таблицю для отриманої формули;
3) якщо ця формула є тавтологією, то з Р, логічно випливає її (Б, Ь Б2); якщо ця формула не є тавтологією, то з Б, логічно не випливає Р2
Нехай Р, - (АлВ), а Р2 - (А/В). Перевіримо, чи є ¥2 логічним наслідком Б,.
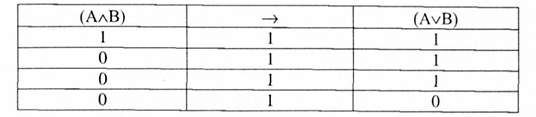
Оскільки отримана формула є тавтологією, то це означає, що Р, ьР2. Перевіримо тепер навпаки: чи є Р, логічним наслідком Р2.
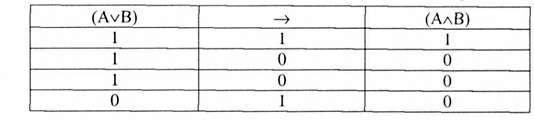
Оскільки ця формула не є тавтологією, то це означає, що Р, не є логічним наслідком з Р2
Якщо Р1ЬР2, але ¥2*¥19 то формула Р, є більш сильною по відношенню до Р2. Якщо ж Р, І-Р2 і $2і-¥1, то Р1 та Р2- рівносильні або еквівалентні.
Література для поглибленого вивчення розділу
А. Основна.
1. Гетманова А. Д. Логика. - М.: Новая школа, 1995. - С. 68-83.
2. Жеребкін В. Є. Логіка. - X.: Основа; К.: Знання, 1999. - С. 86-93.
3. Кириллов В. И., Старченко A. A. Логика. - М.: Высшая школа, 1995. - С. 158-163.
4. Конверський А. Є. Логіка. - К.: Четверта хвиля, 1998. - С. 195-202.
5. Иванов Е. А. Логика. - М: Издательство БЕК, 1996. - С. 137-171.
6. Свинцов В. И. Логика.-М.: Скорина; Весь мир, 1998.-С. 101-116.
7. Тофтул М. Г. Логіка: Навч. посібн. для студентів вищих навчальних закладів. - К.: Академія, 2003. - С. 90-102.
8. Хоменко І. В., Алексюк I. A. Основи логіки. - К.: Золоті ворота, 1996. - С. 96-145.
9. Хоменко І. В. Логіка: Підручник для студентів вищих навчальних закладів. - К.: Абрис, 2004. - С. 99-107.
В. Додаткова
1. Ивин А. А. Искусство правильно мыслить. - М.: Просвещение, 1990. - С. 154-209.
2. Карнап Р. Значение и необходимость. - М.: Наука, 1968. - С. 331-334.
3. Кондаков Н. И. Логический словарь-справочник. - М.: Наука, 1975. Статті: высказывание, дизъюнкция, импликация, исчисление высказываний, конъюнкция, отношение между суждениями, разделительное суждение, сложное суждение, суждение, условное суждение, эквивалентность.
4. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.
5. Мельников В. Н. Логические задачи. - К.; Одесса: Вища школа, 1989. - С. 59-101; 154-177.
6. Свинцов В. И. Смысловой анализ и обработка текста. - М.: Наука 1979.-272 с.
Схожі статті
-
Логіка - Мозгова Н. Г. - 4. Особливості імплікації
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або...
-
Логіка - Мозгова Н. Г. - 3. Відношення еквівалентності між складними висловлюваннями
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або...
-
Логіка - Мозгова Н. Г. - 1. Поняття складного висловлювання
Короткий зміст розділу Складне судження (висловлювання) є об'єктом вивчення розділу логіки, який називають *логікою висловлювань. Логіка висловлювань є...
-
Логіка - Мозгова Н. Г. - 2. Логічні сполучники та логічні операції
Короткий зміст розділу Складне судження (висловлювання) є об'єктом вивчення розділу логіки, який називають *логікою висловлювань. Логіка висловлювань є...
-
Логіка - Мозгова Н. Г. - Розділ 6. Складне судження
Короткий зміст розділу Складне судження (висловлювання) є об'єктом вивчення розділу логіки, який називають *логікою висловлювань. Логіка висловлювань є...
-
Логіка - Мозгова Н. Г. - 6. Логіка й мова
Розглянемо тепер, що таке закон мислення. Для висвітлення цього питання необхідно розрізняти істинність думки та логічну правильність розмірковування....
-
Оскільки кожне судження одночасно має якісну і кількісну характеристику, то буде доцільним об'єднати два попередніх поділи суджень за якістю і кількістю....
-
Логіка - Мозгова Н. Г. - 8. Визначення логіки як науки
Розглянемо тепер, що таке закон мислення. Для висвітлення цього питання необхідно розрізняти істинність думки та логічну правильність розмірковування....
-
Логіка - Мозгова Н. Г. - 7. Поняття штучної мови
Розглянемо тепер, що таке закон мислення. Для висвітлення цього питання необхідно розрізняти істинність думки та логічну правильність розмірковування....
-
Логіка - Мозгова Н. Г. - 7. Відношення суперечності. Закон виключеного третього
Нагадаємо, що несумісними є судження, які не бувають одночасно істинними. Першим видом несумісності є протилежність (контрарність). У відношенні...
-
Логіка - Мозгова Н. Г. - 6. Відношення протилежності. Закон суперечності
Нагадаємо, що несумісними є судження, які не бувають одночасно істинними. Першим видом несумісності є протилежність (контрарність). У відношенні...
-
Логіка - Мозгова Н. Г. - 8. Розподіленість термінів у категоричних судженнях
Оскільки кожне судження одночасно має якісну і кількісну характеристику, то буде доцільним об'єднати два попередніх поділи суджень за якістю і кількістю....
-
Логіка - Мозгова Н. Г. - 5. Поняття закону правильного мислення
Розглянемо тепер, що таке закон мислення. Для висвітлення цього питання необхідно розрізняти істинність думки та логічну правильність розмірковування....
-
Логіка - Мозгова Н. Г. - 6. Виділяюче судження
Дещо стверджувати або заперечувати можна стосовно одного предмета, частини предметів та всіх предметів деякої множини предметів. У залежності від цього...
-
Логіка - Мозгова Н. Г. - 2. Відношення еквівалентності
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Логіка - Мозгова Н. Г. - 1. Поняття про логічні відношення між простими судженнями
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Логіка - Мозгова Н. Г. - 5. Поділ простих суджень за кількістю
Дещо стверджувати або заперечувати можна стосовно одного предмета, частини предметів та всіх предметів деякої множини предметів. У залежності від цього...
-
Логіка - Мозгова Н. Г. - 2. Логічні прийоми утворення понять
Короткий зміст розділу Процес пізнання людиною зовнішнього світу є дуже складним; він включає в себе різні етапи, форми, результати відображення...
-
Логіка - Мозгова Н. Г. - 1. Ознака предмета думки
Короткий зміст розділу Процес пізнання людиною зовнішнього світу є дуже складним; він включає в себе різні етапи, форми, результати відображення...
-
Логіка - Мозгова Н. Г. - Розділ 2. Загальна характеристика поняття
Короткий зміст розділу Процес пізнання людиною зовнішнього світу є дуже складним; він включає в себе різні етапи, форми, результати відображення...
-
Логіка - Мозгова Н. Г. - Мета вивчення логіки
Мета вивчення логіки Навчальний посібник містить вичерпний обсяг теоретичного матеріалу, необхідного для успішного оволодіння програмними знаннями з...
-
Логіка - Мозгова Н. Г. - Розділ 1. Предмет логіки
Мета вивчення логіки Навчальний посібник містить вичерпний обсяг теоретичного матеріалу, необхідного для успішного оволодіння програмними знаннями з...
-
Логіка - Мозгова Н. Г. - МОДУЛЬ 1. ПОНЯТТЯ
Мета вивчення логіки Навчальний посібник містить вичерпний обсяг теоретичного матеріалу, необхідного для успішного оволодіння програмними знаннями з...
-
Логіка - Мозгова Н. Г. - 7. Поділ за видозміною ознаки та його правила
При вивченні деякого поняття перед нами часто виникає питання про необхідність розкриття його обсягу, тобто розподілу предметів, які містяться в понятті,...
-
Логіка - Мозгова Н. Г. - 6. Поділ поняття та його види
При вивченні деякого поняття перед нами часто виникає питання про необхідність розкриття його обсягу, тобто розподілу предметів, які містяться в понятті,...
-
Логіка - Мозгова Н. Г. - 5. Неявні визначення та прийоми, подібні до визначення
Визначення повинно бути не тільки істинним за змістом, але й правильним за своєю структурою. Правильність визначення залежить від дотримання певних...
-
Логіка - Мозгова Н. Г. - 4. Правила визначення поняття
Визначення повинно бути не тільки істинним за змістом, але й правильним за своєю структурою. Правильність визначення залежить від дотримання певних...
-
Логіка - Мозгова Н. Г. - 3. Явне визначення
Короткий зміст розділу У цьому розділі ми продовжимо вивчення теми "Поняття" і зупинимося на питаннях логічних операцій з поняттями. До логічних операцій...
-
Логіка - Мозгова Н. Г. - 2. Види визначень
Короткий зміст розділу У цьому розділі ми продовжимо вивчення теми "Поняття" і зупинимося на питаннях логічних операцій з поняттями. До логічних операцій...
Логіка - Мозгова Н. Г. - 5. Відношення логічного слідування