Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 12.5. Графічне розв'язання матричних ігор розміру 2xn, mx2

Графічний метод можна застосовувати до матричних ігор, в яких хоча б один з гравців має тільки дві стратегії.

Розглянемо гру розміром 2 x n, в якій гравець А має дві чисті стратегії А, А2, гравець В - n чистих стратегій В1, В2, Вn. Вважаємо, що гра не має сідлової точки. Позначимо р1 - ймовірність застосування гравцем А стратегії А1, р2 - ймовірність застосування гравцем А стратегії А2, причому р2 = 1 - р1 ; q1 - ймовірність застосування гравцем В стратегії В1, q2 - ймовірність застосування

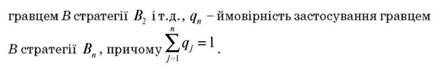
Платіжна матриця цієї гри представлена в табл. 12.11:

Таблиця 12.11 Платіжна матриця гри розміром 2 x n

платіжна матриця гри розміром 2 x n

Якщо гра не має сідлової точки, то за основною теоремою теорії ігор вона має хоча б одне оптимальне рішення, яке визначається

Аналогічно знайдемо очікувані середні виграші гравця А, якщо гравець В використовує чисті стратегії В2, В3Вп, які представимо у табл. 12.12.

Таблиця 12.12. Очікувані виграші гравця А

очікувані виграші гравця а

З таблиці 12.12 видно, що очікуваний виграш гравця А лінійно залежить від рo1 . Побудуємо вирази очікуваних виграшів гравця А.

Гравцю А слід обирати таки стратегії, щоб максимізувати свій мінімальний очікуваний виграш. Тому оптимальна стратегія гравця А визначається як точка перетину прямих, що максимізують його мінімальний очікуваний виграш.

Аналогічно знаходимо оптимальну стратегію гравця В. Вона визначається як точка перетину прямих, що мінімізують його максимальний очікуваний програш.

Таблиця 12.13. Очікувані виграші гравця А

очікувані виграші гравця а

На осі абсцис відкладемо відрізок, довжина якого дорівнює одиниці. Лівий кінець відрізка відповідає стратегії А1, правий - стратегії А2 . Проміжні точки осі абсцис відповідають певним

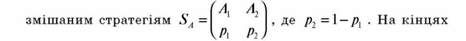
Вибраного відрізку проведемо прямі, на яких будемо відкладати виграш при відповідних чистих стратегіях (рис. 12.6).

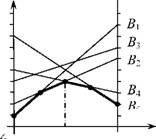
геометрична інтерпретація матричної гри прикладу 12.6

Рис. 12.1. - Геометрична інтерпретація матричної гри прикладу 12.6

З теорії ігрових моделей відомо, що слід взяти нижню огибаючу всіх прямих, що відповідають стратегіям гравця А, яку на рис 12.1 показано жирною ломаною. На цій ломаній, яка завжди обернена опуклістю вверх, знаходимо найбільше значення, яке й буде ціною гри або значенням гри для змішаних стратегій.

Найбільший виграш матиме гравець А, якщо від обере змішану стратегію, що відповідатиме застосуванню гравцем В суміші стратегій В2 і В4. Для знаходження оптимальної стратегії гравця А і ціни гри слід розв'язати систему рівнянь (12.18):

Для знаходження оптимальної стратегії гравця В можна скористатися відомим результатом з теорії: оптимальна стратегія гравця В будується на двох чистих стратегіях, тобто гра 2 x n може бути зведена до гри 2 x 2 .

При використанні графічного метода видно які зі стратегій гравця В відпадають (тобто їх ймовірності дорівнюють нулю: q1 = q3 = q5 = 0 ), а які використовуються з ймовірностями q2 і q4, причому q2 + q4 = 1 .

З рис. 12.1 видно, що стратегії В1 , В3 і В5 не використовуються, тому гру, що розглядається можна звести до матричної гри розміром 2 x 2 , яку представлено платіжною матрицею

Для гравця В середній програш дорівнює ціни грі v = 4 і система для знаходження його оптимальної стратегії має вигляд:

Таблиця 12.14. Платіжна матриця гри розміром m X 2

платіжна матриця гри розміром m x 2

платіжна матриця гри розміром m x 2

Якщо гра не має сідлової точки, то за основною теоремою теорії ігор вона має хоча б одне оптимальне рішення, яке визначається

Аналогічно знайдемо очікувані середні виграші гравця В, якщо гравець А використовує чисті стратегії А2, А3,...,Аm, які представимо у табл. 12.15.

Таблиця 12.15. Очікувані виграші гравця В

очікувані виграші гравця в

З таблиці 12.15 видно, що очікуваний виграш гравця А лінійно залежить від qo1. . Побудуємо вирази очікуваних виграшів гравця А.

Гравцю В слід обирати таки стратегії, щоб мінімізувати свій максимальний очікуваний програш. Тому оптимальна стратегія гравця В визначається як точка перетину прямих, що мінімізують його максимальний очікуваний програш.

Аналогічно знаходимо оптимальну стратегію гравця А. Вона визначається як точка перетину прямих, що максимізують його мінімальний очікуваний виграш.

Приклад 12.7. Знайти графічно рішення гри, яку задано

Таблиця 12.16. Очікувані виграші гравця В

очікувані виграші гравця в

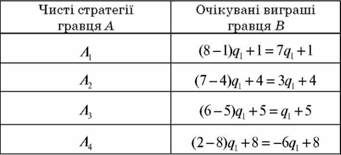
На осі абсцис відкладемо відрізок, довжина якого дорівнює одиниці. Лівий кінець відрізка відповідає стратегії В1 , правий - стратегії В2 . Проміжні точки осі абсцис відповідають певним

Проведемо прямі, на яких будемо відкладати виграш при відповідних чистих стратегіях (рис. 12.2).

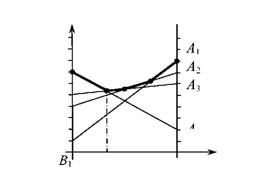
геометрична інтерпретація матричної гри прикладу 12.7

Рис. 12.2. - Геометрична інтерпретація матричної гри прикладу 12.7

З теорії ігрових моделей відомо, що слід взяти верхню огибаючу всіх прямих, що відповідають стратегіям гравця В, яку на рис 12.7 показано жирною ломаною. На цій ломаній, яка завжди обернена опуклістю вниз, знаходимо найменше значення, яке й буде ціною гри або значенням гри для змішаних стратегій.

Найменший програш матиме гравець В, якщо від обере змішану стратегію, що відповідатиме застосуванню гравцем А суміші стратегій А3 і А4. Для знаходження оптимальної стратегії гравця В і ціни гри слід розв'язати систему рівнянь (12.21):

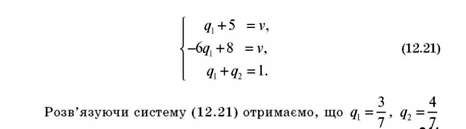
Для знаходження оптимальної стратегії гравця А можна скористаємося відомим результатом з теорії: оптимальна стратегія гравця В будується на двох чистих стратегіях, тобто гра m X 2 може бути зведена до гри 2 x 2 .

З рис. 12.2 видно, що стратегії А1, А2 не використовуються, тому гру, що розглядається, можна звести до матричної гри розміром 2 x 2 , яку представлено платіжною матрицею

Питання для поточного контролю та поглибленого засвоєння знань

1. Охарактеризуйте матричну парну гру.

2. Що називається платіжною матрицею?

3. В чому полягають цілі гравців в матричній парній грі?

4. В чому полягає головний принцип теорії антагоністичних ігор?

5. В чому полягає суть принципу мінімаксу (максиміну)?

6. Що називається нижньою ціною гри?

7. Що таке мінімакс?

8. Як можна скоротити розмірність платіжної матриці?

9. ціною гри?

10. Що таке чиста стратегія гравця?

11. Дайте визначення сідловій точці.

12. Що називається змішаною стратегією гравця?

13. В чому полягає випадковий характер гри?

14. Що представляє собою активна стратегія?

15. В чому полягає суть теореми про активні стратегії?

16. Що представляє собою виграш гравця?

17. Яка стратегія гравця є максимінною?

18. Чому дорівнює середній виграш гравця?

19. Які матричні ігри можна розв'язувати графічно?

20. Якщо гра не має сідлової точки, то чи має вона оптимальне рішення?

21. Як визначається оптимальна стратегія гравця А при графічному розв'язуванні матриної гри?

22. Чи може бути гра 2 x n зведена до гри 2x 2 ?

Схожі статті




Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 12.5. Графічне розв'язання матричних ігор розміру 2xn, mx2

Предыдущая | Следующая