Логіка - Конверський А. Є. - в) Метод аналітичних таблиць

Для подальшого розгляду правил необхідно прийняти деякі домовленості. Аналізуючи правила, природно виникає питання, чи можна перевірити надійність цих правил, їх коректність. На рівні семантики це можна зробити шляхом побудови таблиць істинності, шляхом еквівалентиних перетворень, методом аналітичних таблиць (про що буде сказано пізніше). На рівні синтаксису така перевірка здійснюється через побудову доведення останнього рядка правила.

Розглянемо на прикладі правила транзитивності імплікації його семантичне та синтаксичне обгрунтування (на предмет коректності).

Спочатку зупинимося на семантичному обгрунтуванні.

Побудова таблиць істинності, еквівалентні перетворення (КНФ) досить громіздкі, тому можна запропонувати такий спосіб.

Отже, засновки у нашому правилі не можуть бути істинними, а висновок - хибним, а це свідчить, що це правило логічно коректне і гарантує правильність відповідних його структурі змістовних міркувань.

Схематично така перевірка коректності правила висновку зображується таким чином:

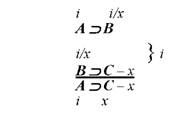
З цієї схеми очевидно, що при будь-яких значеннях В наше припущення про логічну некоректність правила відпадає. У такий, можна сказати, досить економний спосіб можна перевірити кожне з правил.

Синтаксичне обгрунтування правила висновку передбачає побудову виведення останнього рядка із засновків.

Для цього розгорнемо правило, вставивши між засновками і висновком проміжні ланки, які в правилі опущені.

Доведення здійснюється таким способом:

1. Виписуємо засновки, що входять до правила.

2. Зліва виписуємо кроки доведення.

3. Справа напроти кожного кроку виписуємо його підставу (це може бути домовленість про введення чергового припущення, або певне правило). Праву сторону такого запису називають аналізом доведення.

Здійснимо доведення правила ТІ:

Відповідно до цього правила із заперечення диз'юнкції слідує кон'юнкція заперечень висловлювань, що її складають.

Наведемо приклад міркування, побудованого за правилом ЗД:

Читається правило так: "Із заперечення кон'юнкції слідує диз'юнкція заперечень висловлювань, що складають кон'юнкцію".

Наведемо приклад конкретного міркування, що регламентується цим правилом:

Наведемо приклад міркування, побудованого за правилом простої контрапозиції:

Наведемо приклад конкретного міркування за правилом складної контрапозиції:

Наведемо приклад міркування за цим правилом:

Отже, ми розглянули правила висновку логіки висловлювань, які в сукупності є множиною можливих конкретних міркувань. Також з'ясували, що перевірка коректності правила висновку можлива шляхом побудови таблиці істинності для формули, що представляє висновок та доведення останнього рядка правила висновку.

В) Метод аналітичних таблиць.

Окрім цих способів перевірки правила висновку (ми наголошуємо саме на перевірці правила висновку, а не на висновку, саме тому, що будь-який висновок це є по суті втілення конкретного правила висновку, тому перевірка коректності висновку зводиться до перевірки коректності правила висновку) існує ще перевірка шляхом застосування методу аналітичних таблиць.

Основу методу аналітичних таблиць складає звичайне визначення таблиць істинності для пропозиційних зв'язок, а сама аналітична таблиця будується навпаки. Виходимо із того, що значення істинності усього виразу нам відомо, залишається знайти лише значення істинності для елементарних висловлювань, з яких складається цей вираз.

Іншими словами, таблиці називаються аналітичними тому, що розкладаючи вихідне висловлювання на елементарні висловлювання (на атоми), ми намагаємося знайти набір значень атомів, при яких би вихідне висловлювання було хибне.

Розглянемо застосування методу аналітичних таблиць для перевірки коркетності висновку у логіці висловлювань. Наприклад, візьмемо складне висловлювання:

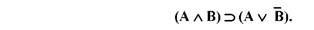
Припустимо, що воно хибне. Якщо в результаті встановлення значення атомів, з яких складається вихідне висловлювання, прийдемо до протиріччя, то цим самим буде аргументована коректність висновку, відображеного в цьому висловлюванні.

Для побудови аналітичної таблиці необхідно виконати такі умови:

1. Нумерацію рядків таблиці розпочинають з 0 (нуля).

2. Наслідки відділяються від припущення горизонтальною рискою.

3. Наслідки, які отримані із одного з попередніх висловлювань позначають римськими цифрами.

4. Аналітична таблиця складається з гілок. Таблиця вважається замкненою, якщо в ній зустрічається пара висловлювань ТА і ТА, а вся аналітична таблиця вважається замкненою, коли кожна її гілка замкнена.

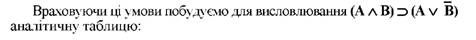
Замкненість аналітичної таблиці позначається знаком (+) (у нашому прикладі після 7 рядка). Отже, наведене висловлювання тотожно істинне, припущення про його хибність відпадає і можна стверджувати, що дане складне висловлювання коректне відносно правил висновку логіки висловлювань.

Розглянемо складніший випадок.

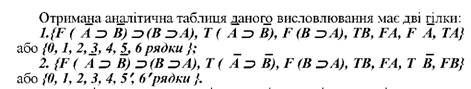
Перша гілка замкнена, оскільки в ній наявні рядки 4 і 6 з висловлюваннями FА і ТА. Замкненою є і друга гілка з рядками 3 і 6'з висловлюваннями TB i FB. Отже, вся аналітична таблиця є замкненою.

Якщо висновок логіки висловлювань неправильний, то при побудові аналітичної таблиці отримаємо хоча б одну незамкнену гілку. Побудуємо аналітичну таблицю висловлювання:

Отже, дане висловлювання не є тавтологією, а це означає, що воно має неправильний висновок.

Схожі статті




Логіка - Конверський А. Є. - в) Метод аналітичних таблиць

Предыдущая | Следующая